対応分析(第2回) スモールアンケートデータで実践
対応分析の基本形
とにかくやってみる
対応分析とは?数量化理論Ⅲ類の分析手法です。対応分析・数量化理論Ⅲ類をネットで調べても数学的すぎて理解できない!私自身がそうなのです。数学的素養ほぼゼロの私が対応分析・数量化理論Ⅲ類を説明することは不可能なのです。それでも実践しているうちに、何となくこんな感じのものかなぁというのがみえてきました。
サンプルデータ
テーブルごとスクレイピングして実践してみてください。
| 好きな食べ物 | 年代 | 回答者 |
| イチゴ | 10代 | A |
| イチゴ | 10代 | B |
| ミカン | 20代 | C |
| ミカン | 20代 | D |
| バナナ | 30代 | E |
| バナナ | 30代 | F |
データは好きな果物を聞いたアンケート調査結果です。
回答者は6名、回答者の年代がわかっていて、10代×2名、20代×2名、30代×2名です。
分析をするまでもなく10代はイチゴ、20代はミカン、30代はバナナが好きであることは明白です。それでもやってみます。
アイテムスコア
上表を使いアイテムスコアを算出します。
ご覧のとおり上表には値がありません。数量化理論Ⅲ類は数値ではないデータを分析きできる、たとえば文字列を数値化して分析する手法ことができます。
| 10代 | 20代 | 30代 | |
| イチゴ | 2 | 0 | 0 |
| バナナ | 0 | 0 | 2 |
| ミカン | 0 | 2 | 0 |
・好きな果物が行
・年代が列のクロス集計表をつくります。
数値は好きな果物の出現回数です。
Rでアイテムスコアを算出します。Rの関数は「corresp」です。
| [成分1] | [成分2] | |
| イチゴ | 0 | -1.41421 |
| バナナ | -1.22475 | 0.707107 |
| ミカン | 1.224745 | 0.707107 |
算出したアイテムスコアです。
アイテムスコアの
・「成分1」を横軸「x」
・「成分2」を縦軸「y」にして散布図を描きます。
プロットする前に「イチゴ」「ミカン」「バナナ」がプロットされる座標から、2点間の距離を算出してみます。
距離=√(x1―x2)^2+(y1―y2)^2
| x差2乗 | y差2乗 | 距離 | ||
| イチゴ | バナナ | 1.5 | 4.5 | 2.44949 |
| イチゴ | ミカン | 1.5 | 4.5 | 2.44949 |
| バナナ | ミカン | 6.000001 | 0 | 2.44949 |
・「イチゴ」と「ミカン」
・「イチゴ」と「バナナ」
・「ミカン」と「バナナ」
これらの距離は全く同じになります。そうなると、これら3点をプロットすると、3点は正三角形を描くはずです。
カテゴリースコア
| イチゴ | バナナ | ミカン | |
| 10代 | 2 | 0 | 0 |
| 20代 | 0 | 0 | 2 |
| 30代 | 0 | 2 | 0 |
今度は年代を行にしたクロス集計表をつくります。
同じようにRへ投入してカテゴリースコアを算出します。
| [成分1] | [成分2] | |
| 10代 | 0 | -1.41421 |
| 20代 | -1.22475 | 0.707107 |
| 30代 | 1.224745 | 0.707107 |
アイテムスコアと全く同じ数値になりました。当然ですが各2点間の距離も等しくなります。
描画します
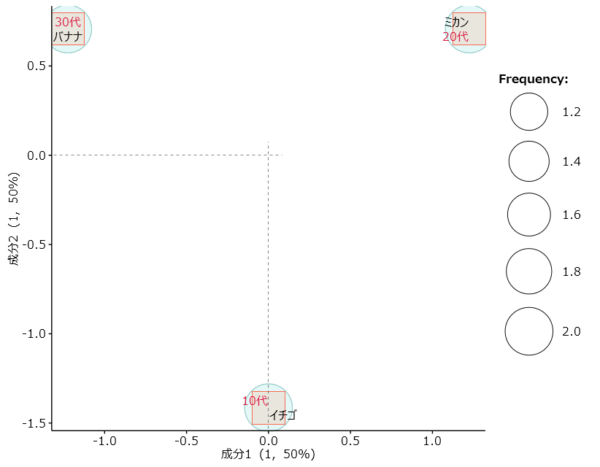
アイテムスコアを青い丸、カテゴリースコアは赤い四角でプロットしました。
イチゴのアイテムスコアと10代のカテゴリースコアはまったくの同一値ですから、同じ位置へプロットされます。
結果
・10代はイチゴ
・20代はミカン
・30代はバナナが好きな果物である、という結果です。
予想通り当たり前の結果です。データを見たときにすでにわかっていました。サンプルデータは6行だけでした。もしもデータがビッグで数百数千もあると見ただけではわかりません。
複数回答MA
サンプルデータ
| 好きな食べ物 | 年代 | 回答者 |
| イチゴ、バナナ | 10代 | A |
| イチゴ | 10代 | B |
| ミカン、イチゴ | 20代 | C |
| ミカン | 20代 | D |
| バナナ、イチゴ | 30代 | E |
| バナナ | 30代 | F |
回答者Aにバナナ、回答者Cにイチゴ、回答者Eにもイチゴを加えました。
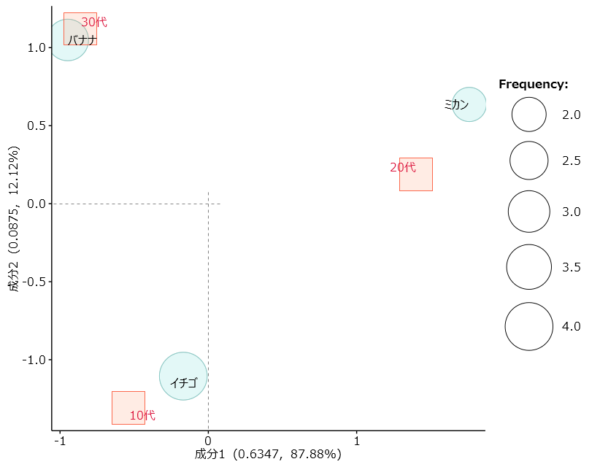
青い丸(アイテムスコア)のサイズ変化
青い丸のサイズに変化があります。
青い丸のサイズは全体のなかでそれぞれの「語」が出現する回数に比例して大きく・小さくなります。サイズが変わったということは、「語」の出現回数が変わったということです。
イチゴの出現回数が2回増加し4回へ、バナナは1回増加し3回へ、ミカンは2回で変化なし。
サイズが大きい順に並べると「イチゴ」「バナナ」「ミカン」の順にまりますね。
赤い四角(カテゴリースコア)の位置変化
青い丸も赤い四角も前回から位置が変化しています。
ただし、赤い四角の位置は変化しましたが2点間の距離は同じなのです。
赤い四角3点は相変わらず正三角形を描き、各辺の長さに変化はありません。座標は変化したが、赤い四角と赤い四角の位置関係という意味では全く同一です。
| [成分1] | [成分2] | |||
| 10代 | -0.53783 | -1.30795 | ||
| 20代 | 1.401634 | 0.188205 | ||
| 30代 | -0.86381 | 1.119748 | ||
| x差2乗 | y差2乗 | 距離 | ||
| 10代 | 20代 | 3.76151 | 2.238491 | 2.44949 |
| 10代 | 30代 | 0.106263 | 5.893737 | 2.44949 |
| 20代 | 30代 | 5.132227 | 0.867773 | 2.44949 |
各赤い四角の位置関係が変化しません。このあたりに対応分析と主成分分析との違いがあるようです。
対応分析では似ているところはより近く、違うところはより遠く表現します。
外部変数が3の場合はできるだけ正三角形を描き、画面全体で表現するように工夫されているみたいです。
青い丸の位置変化
| [成分1] | [成分2] | |||
| イチゴ | -0.16877 | -1.10522 | ||
| バナナ | -0.94787 | 1.04954 | ||
| ミカン | 1.759356 | 0.636134 | ||
| x差2乗 | y差2乗 | 距離 | ||
| イチゴ | バナナ | 0.606999 | 4.643001 | 2.291288 |
| イチゴ | ミカン | 3.717679 | 3.032321 | 2.598076 |
| バナナ | ミカン | 7.329095 | 0.170905 | 2.738613 |
見た目で位置の変化を読みとることができるので、距離も変化していることを確認しました。
ここで重要なのは距離が示す数値ではなく、位置と距離の両方が変化しているということだけです。
距離が違うのでプロットしたときに正三角形にはなりません。
青い丸の位置関係が変化する理由
位置の変化は「語」が出現する場所(データが属しているカテゴリー)が変化したからです。
10代だけに出現していたイチゴが20代と30代にも出現します。
従って20代を示す赤い四角と30代を示す赤い四角に引っ張られて原点ゼロ方向に移動します。
出現回数は10代で2回、20代で1回、30代で1回ですからまだ10代に近い位置にあります。「語」が出現する回数が多い青い四角に近づきます。
バナナは30代から20代方向へ動きます。
出現回数は30代で2回、10代で1回ですから30代に近いポジションになります。20代には出現しないので20代の方向へは移動しません。
ミカンが出現するのは20代だけです。
従って、原点ゼロからみて20代の赤い四角の外側へ移動します。移動すると言うより、はじき出されるといったほうが的確かもしれません。
このように対応分析は
データの数量と場所をあらわすこと
このように考えてよいと思います。
主成分分析との違い
主成分分析
| 10代 | 20代 | 30代 | |
| イチゴ | 2 | 1 | 1 |
| バナナ | 1 | 0 | 2 |
| ミカン | 0 | 2 | 0 |
主成分分析用のデータです。複数回答MAのデータをクロス集計しました。このデータをRへ読み込んで結果を算出します。
#CSVデータの読み込み
d = read.csv('ファイルパス/ファイル名.csv',head=T,row.names=1)
#主成分分析実行
d_pr = prcomp(d, scale=T)
# 主成分分析結果を表示
d_pr
#結果をプロット
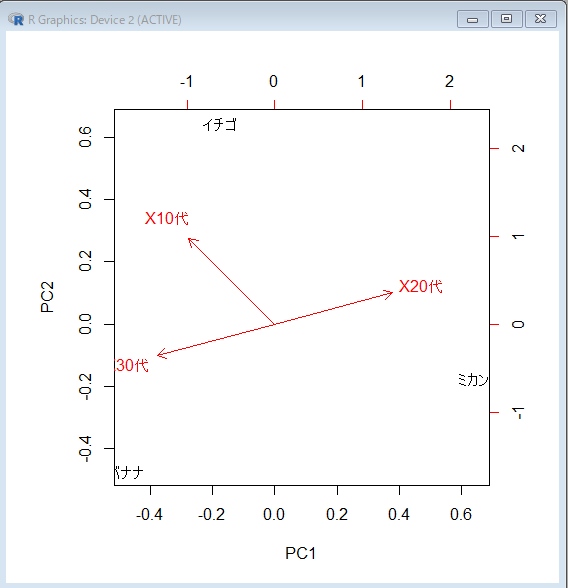
biplot(d_pr)主成分分析結果
対応分析とは違う描画になりました。年代の位置関係が正三角形ではありません。
20代と30代が、まったく反対側にプロットされるのは、
・20代には「バナナ」が含まれない
・30代には「ミカン」が含まれない
つまり共通する成分が「イチゴ」ただ1個だけだからです。
10代と30代が近いのは、ともに「ミカン」を含まず「イチゴ」「バナナ」の2個が共通成分になっているからです。
対応分析結果と比較すると「イチゴ」「ミカン」「バナナ」の位置が違います。これは対応分析が関連性が強くて似ているものが近くになるよに値を算出しているからです。
元の情報をそのままビジュアル化するのが主成分分析,似ているとか違うとかを見つけるのが対応分析ですね。