クラスター分析とは

好きな食べ物

日本人が好む食事といえば寿司だそうです。すしネタのなかでは、まぐろ、サーモン、いくら、はまち、えび、このあたりが人気上位を占めるみたいです。

とは言ってもすし店に来店される顧客の全員がまぐろ好きとは限りません。まぐろは苦手という顧客もいるし、まぐろしか食べないというよな顧客もいるはずです。好きなすしネタ、苦手なすしネタのような顧客別の嗜好ですし店の顧客を特徴づける方法がクラスター分析です。

クラスター分析が有効な場面

回転すし店を予約しようと思います。近隣には回転すし店が３店舗あってどこにしようかと迷います。回転すし店のスマホアプリを開いてみると、１店舗目は「まぐろ１皿無料クーポン」、２店舗目は「サーモン１皿無料クーポン」、３店舗目は「フライドポテト100円値引クーポン」です。まぐろ好きは１店舗目、サーモン好きは２店舗目、お子様連れは３店舗目を予約すると思います。

すし店がアプリを開いた顧客の嗜好をあらかじめ知っているとしたら？１店舗目をまぐろ好きが開くと「まぐろ１皿無料クーポン」、１店舗目をサーモン好きが開くと「サーモン１皿無料クーポン」、１店舗目をお子様連れが開くと「フライドポテト100円値引クーポン」ですね。１店舗目を予約します。

２軸クラスター分析

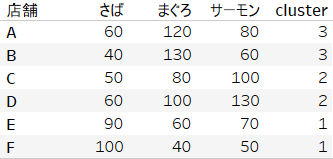
サンプルデータ

顧客グループ	さば	まぐろ	サーモン	合計
A	60	120	80	260
B	40	130	60	230
C	50	80	100	230
D	60	100	130	290
E	90	60	70	220
F	100	40	50	190
合計	400	530	490

顧客グループ：A,B,C,D,E,F
商品データ：３種類　さば、まぐろ、サーモン
数値：食べた皿数

クラスター分析

分析ツール：タブロー

食べた皿数で２軸を設定して、顧客グループをプロットした散布図をつくります。クラスター分析のスタートは２軸からです。顧客たいして二者択一の質問をするイメージです。
３種類の商品から２軸をつくると、さばorまぐろ、さばorサーモン、まぐろorサーモン、これら３通りのの組み合わせができます。クラスター数を指定せず、タブローにおまかせ状態ですから、階層クラスター分析になります。

分析結果をアナログで表現するとこのような感じです。

顧客グループ	さばorまぐろ	さばorサーモン	まぐろorサーモン
A	まぐろ	はっきりしない	まぐろ
B	まぐろ	はっきりしない	まぐろ
C	まぐろ	サーモン	どちらも好き
D	まぐろ	サーモン	サーモン
E	さば	さば	はっきりしない
F	さば	さば	はっきりしない

ここであることに気付きます。「Ａ・Ｂ」は常に同じクラスターになり、「Ｅ・Ｆ」も常に同じクラスターになります。ＣとＤは「Ａ・Ｂ」のクラスターになったり、別のクラスターにもなり、ＣとＤが分かれることもあります。

質問にたいする回答

質問①：さば、まぐろ、どちらが好きですか？
質問②：さば、サーモン、どちらが好きですか？
質問③：まぐろ、サーモンどちらが好きですか？

Ａ・Ｂは常に同じクラスターになり、Ｅ・Ｆも常に同じクラスターになるということは、二者択一の３つの質問にたいして「Ａ・Ｂ」と「Ｅ・Ｆ」はいつも同じ答えをしているから常に同じクラスターになるようにみえます。

さばorまぐろorサーモン

全部盛り

データは同じですから、質問と選択肢はこのようになります。
質問：さば、まぐろ、サーモン、どれがが好きですか？
分析ツールＲ

#データを読み込みます
d2<-read.csv("ファイルパス/ファイル名.csv",header=T)
#店舗を列名にします
row.names(d2) = d2[,1]
#データの２列目から４列目を分析します
#アイテム数が多い場合は分析する列数を増やすだけでＯＫです
d2 = d2[,2:4]
#距離を計算します
d.dist<- dist(d2)
#クラスターを形成します
d.hc1<-hclust(d.dist,method="ward.D")
#デンドログラムを描画します
plot(d.hc1)

結果

デンドログラム（樹形図といわれています）で描画しました。（左右は同じものです）
右図①の赤い線で分割するとクラスターは２になります。
「さばorまぐろ」でクラスターをつくったときと同じ結果になります。

右図②の赤い線で分割するとクラスターは３になります。
「さばorサーモン」でクラスターをつくったときと同じ結果になります。

右図③の赤い線で分割するとクラスターは４になります。
前回の「まぐろorサーモン」と同じ結果になります。

結果が同じということは、アイテム数「or」をどんどん増やしてもアルゴリズムはまったく同じだろうということです。

何を計算してクラスターを形成しているのか

	A	B	C	D	E
B	30
C	45.82576	64.80741
D	53.85165	78.74008	37.41657
E	67.8233	86.60254	53.85165	78.1025
F	94.33981	108.6278	81.24038	107.7033	30

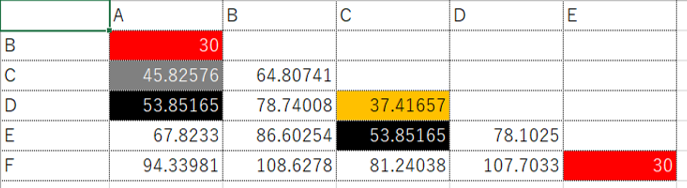
Ａ、Ｂ、Ｃ、Ｄ、Ｅ、Ｆ、それぞれの２点間の距離をあらわします。（６×５）÷（２×１）＝１５通りの距離を算出します。

＜第１段階　③の線＞
２点間の距離が最も近いＡ・ＢとＥ・Ｆ（赤いセル）のクラスターが同時に形成されます。同時というのはどちらも距離が同じ（３０）だから、図では同じ高さのところでＡ・ＢとＥ・Ｆのクラスターが形成されました。ＣとＤはくっついていませんからこの時点でのクラスター数は４です。

＜第２段階　②の線＞
次に距離が近いＣ・Ｄ（オレンジのセル）でクラスターが形成されます。時点でのクラスター数は３です。

＜第３段階　①の線＞
その次に距離が近いＡ・Ｃ（グレーのセル）がクラスターを形成します。Ａは第１段階でＢとクラスターを形成、Ｃは第２段階でＤとクラスターをすでに形成していますから、Ａ・Ｂ・Ｃ・Ｄでクラスターが形成されます。時点でのクラスター数は２。言い換えるとＡとＣの仲が良いからＡ・Ｂ・Ｃ・Ｄがまとまっている。

＜最終段階　母集団＞
さいごはＡ・ＤとＣ・Ｅ（黒のセル）がくっついて母集団になります。

決定木分析との違い

決定木分析でもクラスター分析結果のような樹形図をアウトプットしました。どちらも似ていますが決定的な違いがあります。決定木分析は母集団を順次切り離す、樹形図の上から純度が高いノードを分離してゆく手順です。クラスター分析は似ているデータを集める、樹形図の下から積み上げてゆく手順です。ですからクラスターは「分ける」ものではなく「形成する」ものですね。

タブローとＲの連携

Ｒ側でRserveパッケージをつかいかます

install.packages(Rserve)
library(Rserve)
Rserve()

Ｒを起動しておく必要があります。

タブロー側

「ヘルプ」→「設定とパフォーマンス」→「外部サービス接続の管理」

計算式でメジャーをつくります

SCRIPT_INT('set.seed(42);result <- kmeans(data.frame(.arg1,.arg2,.arg3),.arg4[1]);result$cluster;',
SUM([さば]), SUM([まぐろ]),SUM([サーモン]),[clust])

さいごの[clust]はパラメーターです。クラスター数を設定する（非階層クラスター分析）と便利です。

＞クラスター分析(第2回)　クラスターの特徴