TFとは

ＰＰＡＰ

　分析について、数人のまえで話をすることがあります。テキストマイニングの説明をするときに、例題として、ペン、パイナップル、アップル、ペンなんかを使うのですが全くウケません。まじめな席であまりにも言葉が軽いのか、そもそもネタが古すぎるのでしょうか。

　ＴＦ・ＩＤＦは文書中に出現する「語」へ重みをつけようという試みです。
　重い「語」というが何なのか？単純に考えると、文書中に頻繁に出現する「語」、あるいは文書の結論部分に出現する「語」だろうと想像できます。

　コンピューターは「語」の出現回数をあっという間に計算できます。しかし、文書の結論が何なのか、あるいは結論が文書全体のなかのどこにあるのかを見つけ出すことができません。コンピューターは文書を理解することができないからです。

　ＴＦ・ＩＤＦは
・「語」の出現回数が多ければ「重い」という考え方（ＴＦ）
・「語」の出現回数は少ないけれども「重い」だろうと計算される「語」の指数（ＩＤＦ）
　これら２つの考え方をミックスした数値です。ただし、ここで言う「重い」というのは読み手の心にずっしりと響く「語」であるのかというとそうではありません。
　というのも一方の指数ＩＤＦがあくまでも計算式で算出されるだけのものだからです。

データ

text	No.
ペン、パイナップル、アップル、ペン	1
ペン、パイナップル、オレンジ、マンゴー	2
ペン、ストロベリー	3

　まず、KHcoderを使います。使うといっても今回はテキストを読み込んで「語」のマトリクス抽出するところまでです。

　データのようにあらかじめ「段」へＮｏ．を付与しておきます。Ｎｏ．の列がtextの外部変数になります。

　KHcoderへテキストをロードします。
・「前処理の実行」まえに「語の取捨選択」で「使用しない語の指定」へ「、」（読点）を入れてください。
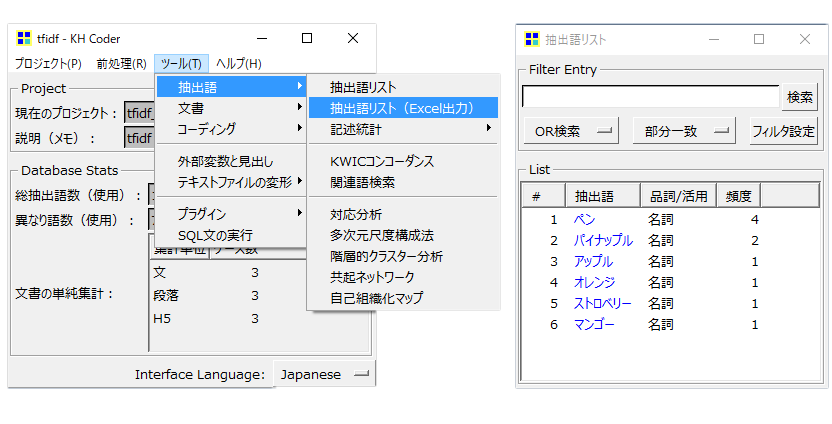
・「ツール」→「抽出語」→「抽出語リスト」で「語」がうまく抽出できているかを確認します。
　画像のように６「語」が表示されていればＯＫです。

TF計算

　ロードしたテキストを行を「段」列を「語」にしたマトリクスへ変換して抽出します。
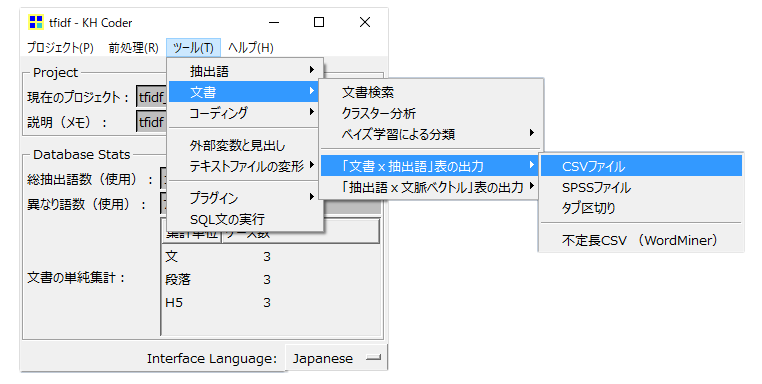
・「ツール」→「文書」→「文書×抽出語」表の出力
・ＣＳＶ形式で保存します。
　KHcoderの役割はここまでです。

＜ＴＦの計算式＞
ＴＦ＝「１文中における語の出現回数」÷「１文の総語数」

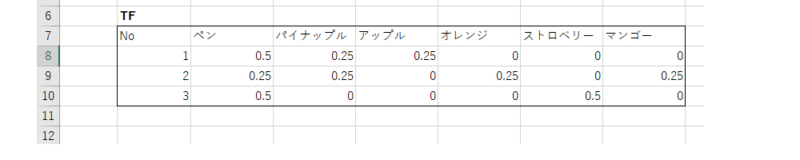
　分子になる「１文中における語の出現回数」は、列Ｃ～Ｈの数値です。
　例えば
・「ペン」はＮｏ．１の文書に２回出現しています。

　分母になる「１文の総語数」は
・列Ｂの「length=w」の数値です。（「使用しない語の指定」へ「、」（読点）を入れていないときに「length=w」の数値が正確でないことがあります）

従って、
Ｎｏ．１の文書で「ペン」のＴＦ＝２（出現回数）÷４（Ｎｏ．１の総語数）＝0.5
　特定の「語」が文書に占める構成比のようなものです。

・ＴＦは１文書を構成する「語」数が少なく、特定の「語」の出現回数が多いほど大きくなります。

　ある文書のなかでＴＦ値が大きいほど重要な「語」であるという定義が成立するのであればテキストマイニングにおいてＴＦ値は重要な意味を持ち得ます。

IDFについて

IDF計算

＜ＩＤＦの計算式＞
ＩＤＦ＝log(「全文書数」÷「語が出現する文書数」)＋１

・「全文書数」は、textの行数合計ですから常に３です。
・「語が出現する文書数」は、５行目のcount数です。

　例えば「ペン」は文書Ｎｏ．１、２、３のすべてに出現するから３です。「ペン」が文書全体のなかで出現する回数４ではないことがポイントです。
　「パイナップル」は文書Ｎｏ．１、２に出現するから「語が出現する文書数」は２になります。

・ＩＤＦは特定の「語」が出現する文書数が少ないほど大きくなる
・特定の「語」が出現する文書数が多いほど小さくなります。

　つまり、まれに出現する「語」がその文書を特徴づけている、そのような「語」が重要な「語」であるという定義が成立すのであれば、ＩＤＦ値が大きい「語」が重要な「語」として意味をもちます。

　ＩＤＦ値が大きい「語」が読み手の心に響く重い「語」であるのかどうかをコンピューターは判断できません。それを判断するのはあくまで読み手です。

ＴＦとＩＤＦの違い

　ＴＦ値とＩＤＦ値は概ね反対方向に動きます。
　それではＩＤＦはＴＦの反対のものだと思いやすいのですが、反対のものではありません。別のものなのです。

・ＴＦの計算式は「語」が出現する回数
・ＩＤＦの計算式は「語」が出現する「文書数」で成り立っています。

　ですからＴＦは文書ごとに算出します。
・Ｎｏ．１の文書の「ペン」のＴＦは0.5
・Ｎｏ．２の文書の「ペン」のＴＦは0.25、このようになります。

　ＩＤＦは文書ごとではなく、「分析対象テキスト」全体のなかで「語」ごとに１値だけを算出します。「語」の出現回数と「語」が出現する「文書数」の違いはテキストマイニングでよく認識間違いされるところです。

・ＴＦは多く出現する「語」によって文書を分別するための道具
・ＩＤＦはまれに出現する「語」によって文書を分別するための道具だといえます。

TF-IDFとは

計算式

ＴＦ・ＩＤＦ＝ＴＦ×ＩＤＦ

　ＴＦ・ＩＤＦは、
・多く出現する「語」によって文書を分別するための道具であるＴＦと
・まれに出現する「語」によって文書を分別するための道具であるＩＤＦ
　これら両方を同時に使ってみた！ものです。

　大きくなる指数と小さくなる指数なら、掛け算をすればいい感じになるだろうという、論理的にはかなり大胆なものです。

　実際にＴＦ・ＩＤＦを算出すると、
・Ｎｏ．３文書の「ストロベリー」のＴＦ・ＩＤＦ値が高くなります。

　「アップル」「オレンジ」「マンゴー」「ストロベリー」の出現回数はいずれも１回です。

　「ストロベリー」のＴＦ・ＩＤＦ値が大きくなる理由は、
・「ストロベリー」が出現する文書No.3の総語数が少ない（２語）から、それだけです。

・「アップル」「オレンジ」「マンゴー」「ストロベリー」のＩＤＦ値はすべて2.58です。
・「アップル」「オレンジ」「マンゴー」のＴＦ値はすべて0.25です。
・Ｎｏ．３文書の「ストロベリー」だけＴＦ値が0.5です。
　その結果、Ｎｏ．３文書の「ストロベリー」のＴＦ・ＩＤＦ値が高くなります。

　それではＴＦ・ＩＤＦ値が高い「ストロベリー」とい「語」自体が何か心に響く重い「語」なのかどうか。このあたりの判断はとても難しいですね。

　では「ストロベリー」を含むＮｏ３．の文書に何か特徴があるのか？
　３段のテキストを比べると感覚的にＮｏ．３の文書はＮｏ．１、２と比較して少し違うように思います。

　結局、ＴＦ・ＩＤＦは「語」の重さをあらわすとしても、”重さ＝心に響く”ではなく、”重さ＝「語」と「語」の違いをあらわす数値”、「語」と「語」の違いをスケールにして文書の違いをはかる道具だといえそうです。

ペン、ペン、ペン・・・

・文書No.1へ「ペン」を100回出現させます。
・文書No.1の「ペン」のTF＝100÷102=1.0です。
・「ペン」のＩＤＦ＝log(3÷3)＋１=1.0です。
・文書No.1の「ペン」のＴＦ・ＩＤＦ＝１×１＝１です。

　ＴＦ＝文中における語の出現回数÷文の総語数ですから、ＴＦ値が1.0を超えることはありません。

　またＩＤＦ＝log(全文書数÷語が出現する文書数)＋１ですから、１文書内における語の出現回数とは無関係です。

　何度も何度も同じ「語」を繰り返されると「語」が重くなるどころか軽くなってしまいます。「しつこいから、もうええわ」のところでストップしているわけです。

・結果として文書No.3に１回だけ出現する「ストロベリー」よりも「ペン」のＴＦ・ＩＤＦ値は小さくなります。
・また、文書Ｎｏ．１の「パイナップル」「アップル」のＴＦ・ＩＤＦがゼロになります。

　これはＮｏ．１の「パイナップル」「アプル」のＴＦ値がほぼゼロになるからです。会議に、やかましいオッサンが１人いて他のひとの意見がかき消されている状況です

ということは、
① ＴＦ・ＩＤＦ値が１以下かつ１に近い値の特定の「語」が出現する文書。
　例えば
・「ペン」が100回出現する文書と「ペン」が99回出現する文書は似ている。
・「ペン」が100回出現する文書と「パイナップル」が100回出現する文書には違いがある。

② ＴＦ・ＩＤＦ値が１を超える「語」を含む文書。
・「ペン」が100回出現し「ストロベリー」が１回出現する文書と「ペン」が１回・「ストロベリー」も１回出現する文書には違いがある。

③ ＴＦ・ＩＤＦ値が高い「語」が違う文書。
　例えば
・「アップル」のＴＦ・ＩＤＦ値が高い文書と「ストロベリー」のＴＦ・ＩＤＦ値が高い文書には違いがある。

④ 複数の文書を比較して特にＴＦ・ＩＤＦ値が高い「語」がないとき。
・ＴＦ・ＩＤＦで分類することができない。