KHcoder 23. 共起ネットワーク(共起パターンの変化を探る)
KHcoder「3.Alpha.16f」に突然出現した「共起パターンの変化を探る」について解説しています。
テキストマイニングツール「KHcoder」の活用メモ
開発者である樋口先生に感謝!
【今回の分析対象テキストはこちらからコピーできます】
新機能 共起パターンの変化を探る
3.Alpha.16f
KHcoderの新バージョン「3.Alpha.16f」をみていると、共起ネットワークのなかに「共起パターンの変化を探る(相関)」という機能が抽出語・コーディングの両方に追加されています。
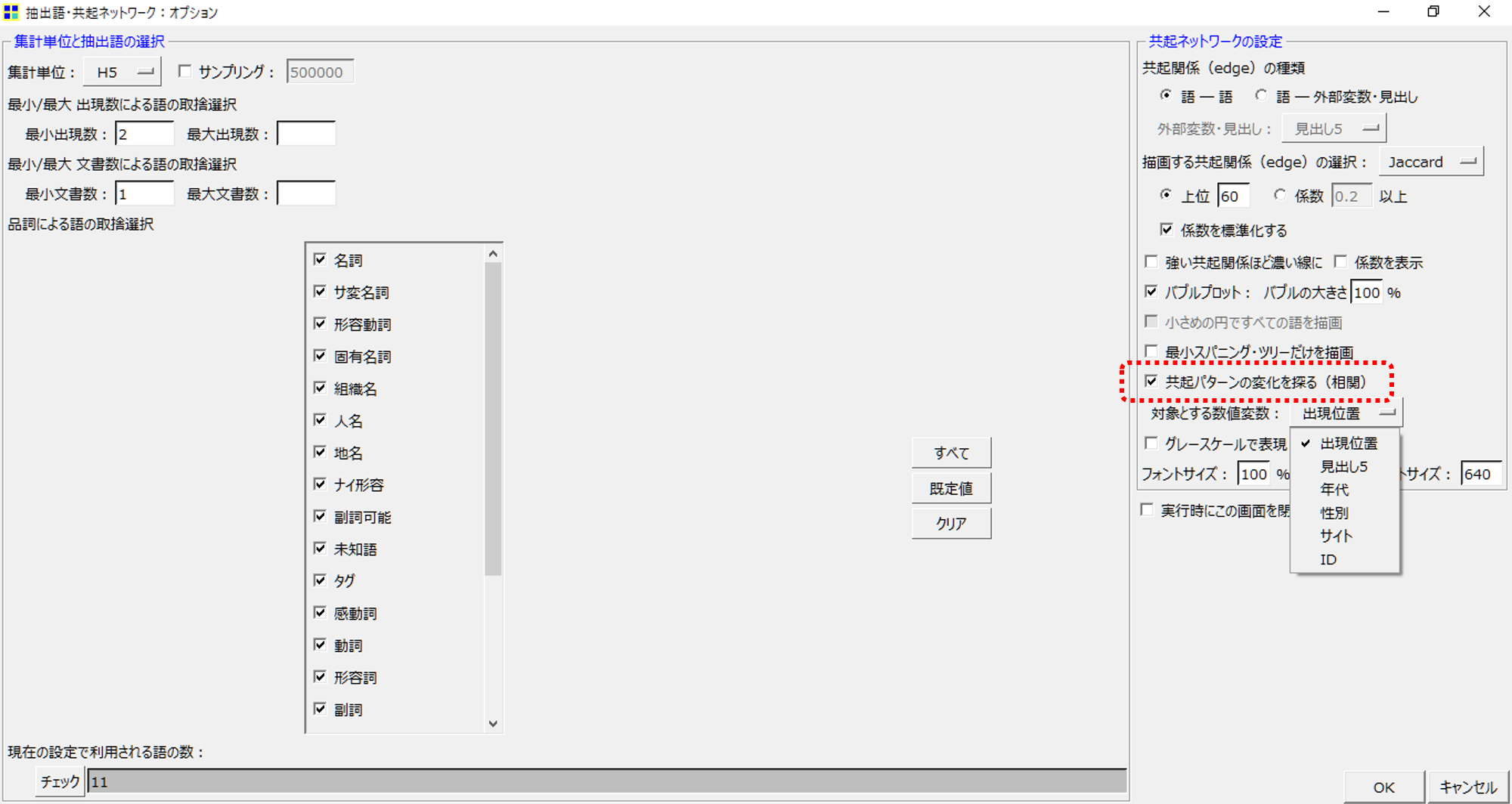
・「共起パターンの変化を探る(相関)をチェック
・「対象とする数値変数」はデフォルトのまま
・「出現位置」でOKします。
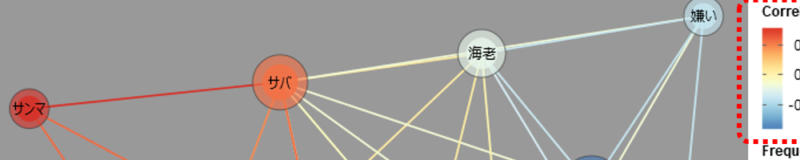
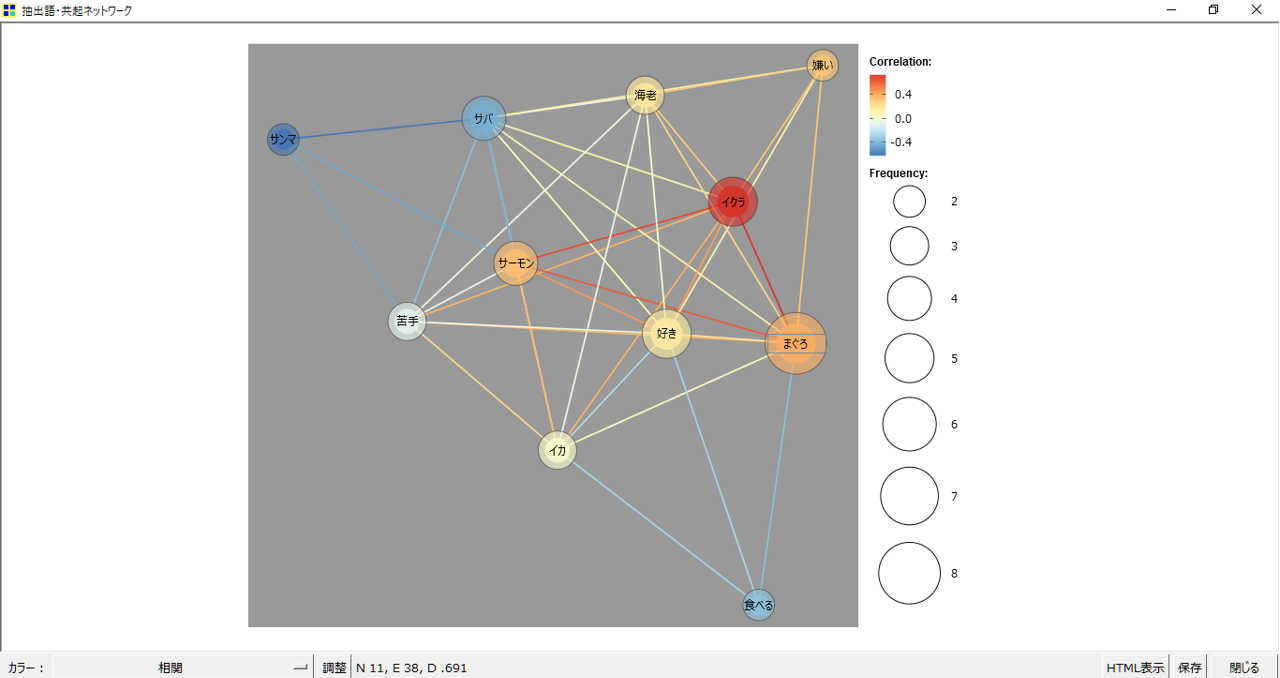
色使いに注目
「共起パターンの変化を探る(相関)をチェックしないときと比較しても、プロット位置、サイズ、線、表示される係数はすべて同じです。
異なるところは色です。
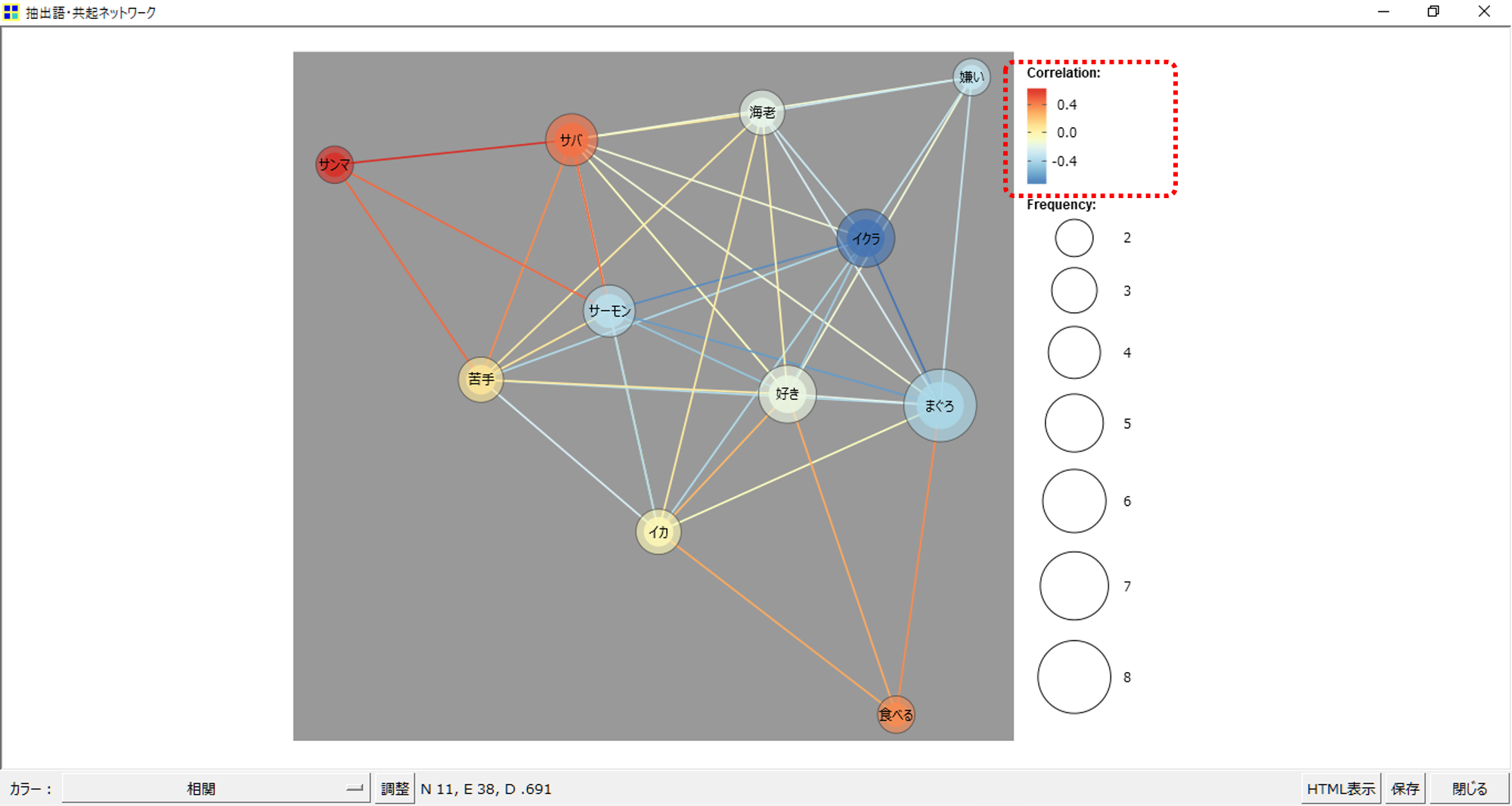
共起ネットワーク図から色相グラデーションは「Correlation」によって決定されることがわかります。
「Correlation」を和訳すると「相関」、では「相関」とは何か?何と何の相関なのか?0.4とか-0.4と表示されている数値は具体的に何なのでしょうか。
Rで確認
「対象とする数値変数」とは
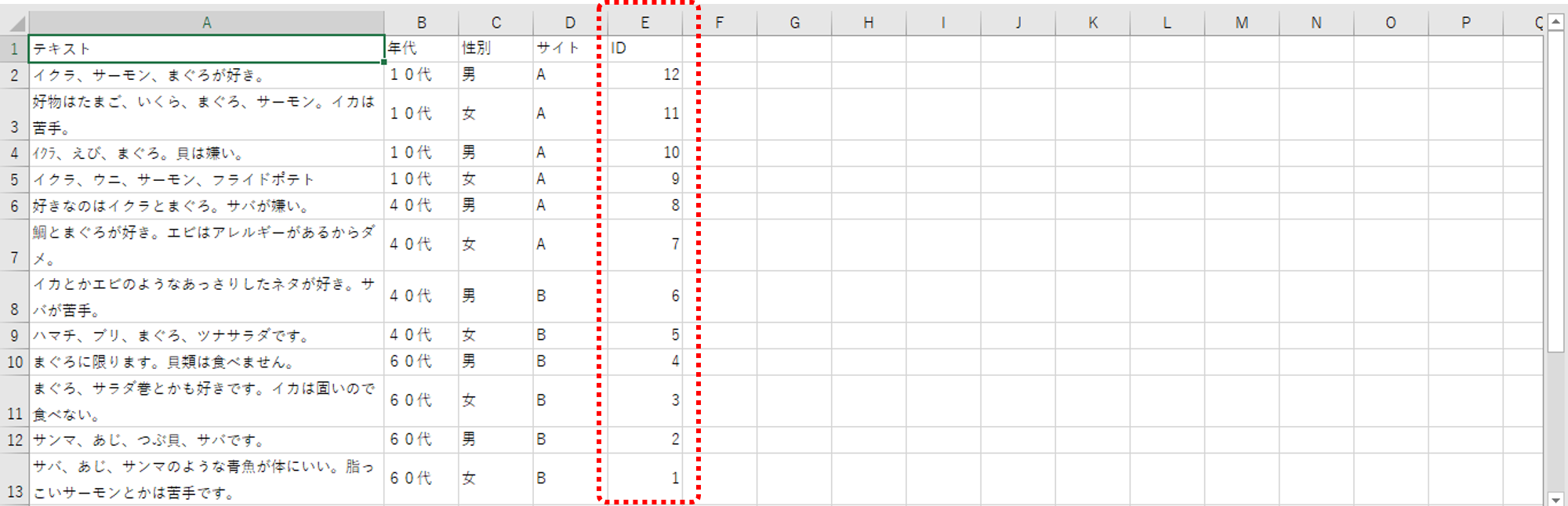
dr サーモン サバ イカ サンマ 好き 苦手 嫌い まぐろ イクラ 海老 食べる khvar_ 1 1 0 0 0 1 0 0 1 1 0 0 1 2 1 0 1 0 0 1 0 1 1 0 0 2 3 0 0 0 0 0 0 1 1 1 1 0 3 4 1 0 0 0 0 0 0 0 1 0 0 4 5 0 1 0 0 1 0 1 1 1 0 0 5 6 0 0 0 0 1 0 0 1 0 1 0 6 7 0 1 1 0 1 1 0 0 0 1 0 7 8 0 0 0 0 0 0 0 1 0 0 0 8 9 0 0 0 0 0 0 0 1 0 0 1 9 10 0 0 1 0 1 0 0 1 0 0 1 10 11 0 1 0 1 0 0 0 0 0 0 0 11 12 1 1 0 1 0 1 0 0 0 0 0 12
・行(row)が「段」
・列(col)のサーモン~食べるまでが「語」です。
・数値はそれぞれの「段」に出現する「語」の出現回数です。
・Rへ送られているデータは、サーモンから食べるまでの列です。
・R内で最終列「khvar_」が追加されます。「khvar_」は数値(値)です。
この「khvar_」が「対象とする数値変数」のことです。
今回は「対象とする数値変数」を「出現位置」に設定しました。
「出現位置」とは分析対象テキストの1段目、2段目、3段目のような、いわゆる「段」番号です。
「段」番号はIDですから基本的には数値(値)ではありません。受験番号のようなユニークな記号です。数字ではなく、アルファベットでもい・ろ・はでも構いません。
相関係数を算出するためには番号を「khvar_」という数値(値)へ変換する必要があります。
相関とはPearson相関係数
cor(dr,method="pearson") サーモン サバ イカ サンマ 好き サーモン 1.0000000 -0.1250000 0.00000000 0.1581139 -0.23904572 サバ -0.1250000 1.0000000 0.00000000 0.6324555 0.11952286 イカ 0.0000000 0.0000000 1.00000000 -0.2581989 0.29277002 サンマ 0.1581139 0.6324555 -0.25819889 1.0000000 -0.37796447 好き -0.2390457 0.1195229 0.29277002 -0.3779645 1.00000000 苦手 0.4082483 0.4082483 0.55555556 0.2581989 -0.09759001 嫌い -0.3162278 0.1581139 -0.25819889 -0.2000000 0.07559289 まぐろ -0.2500000 -0.6250000 0.00000000 -0.6324555 0.23904572 イクラ 0.4780914 -0.2390457 -0.09759001 -0.3779645 -0.02857143 海老 -0.4082483 0.0000000 0.11111111 -0.2581989 0.29277002 食べる -0.3162278 -0.3162278 0.25819889 -0.2000000 0.07559289 khvar_ -0.3584641 0.4608824 -0.02787473 0.6477503 -0.17137861 苦手 嫌い まぐろ イクラ 海老 サーモン 0.40824829 -0.31622777 -0.2500000 0.47809144 -0.40824829 サバ 0.40824829 0.15811388 -0.6250000 -0.23904572 0.00000000 イカ 0.55555556 -0.25819889 0.0000000 -0.09759001 0.11111111 サンマ 0.25819889 -0.20000000 -0.6324555 -0.37796447 -0.25819889 好き -0.09759001 0.07559289 0.2390457 -0.02857143 0.29277002 苦手 1.00000000 -0.25819889 -0.4082483 -0.09759001 0.11111111 嫌い -0.25819889 1.00000000 0.3162278 0.52915026 0.25819889 まぐろ -0.40824829 0.31622777 1.0000000 0.23904572 0.00000000 イクラ -0.09759001 0.52915026 0.2390457 1.00000000 -0.09759001 海老 0.11111111 0.25819889 0.0000000 -0.09759001 1.00000000 食べる -0.25819889 -0.20000000 0.3162278 -0.37796447 -0.25819889 khvar_ 0.08362420 -0.32387514 -0.4096732 -0.85689307 -0.19512314 食べる khvar_ サーモン -0.31622777 -0.35846409 サバ -0.31622777 0.46088240 イカ 0.25819889 -0.02787473 サンマ -0.20000000 0.64775028 好き 0.07559289 -0.17137861 苦手 -0.25819889 0.08362420 嫌い -0.20000000 -0.32387514 まぐろ 0.31622777 -0.40967325 イクラ -0.37796447 -0.85689307 海老 -0.25819889 -0.19512314 食べる 1.00000000 0.38865017 khvar_ 0.38865017 1.00000000
RでPearson相関係数を算出します。関数は「cor」です。
計算結果の最終列「khvar_」列の数値がサーモン~食べるまでの「語」と「khvar_」とのPearson相関係数です。
これが共起ネットワーク図の色(「Correlation」)です。
つまり、「Correlation」(相関)というのは、「語」と「khvar_」との相関をあらわします。
「khvar_」=「出現位置」だから「語」と出現位置との相関です。
外部変数でやってみる
外部変数が数値のとき
分析対象テキストには「外部変数」として「ID」があります。先ほどは「対象とする数値変数」を「出現位置」に設定しましたが、今度は「ID」に設定します。
「出現位置」と同じ結果になります。「出現位置」=「段」番号=「ID」ですから当然です。
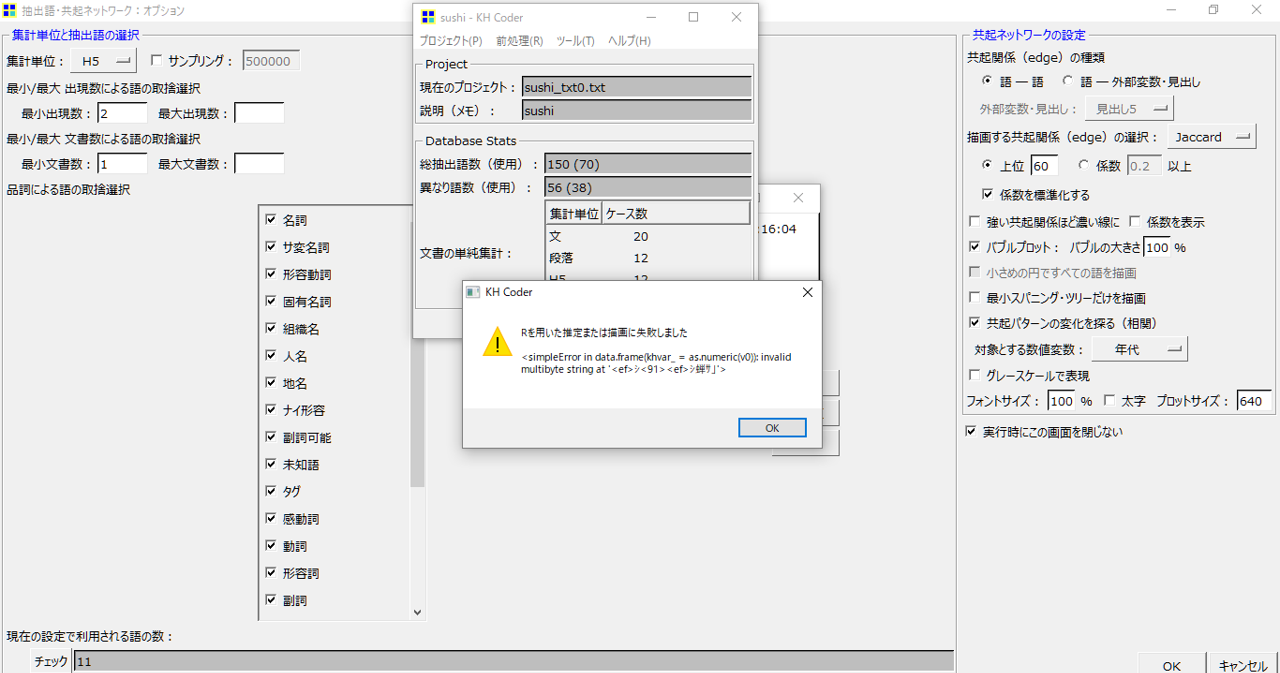
外部変数が文字列のとき
「外部変数」が文字列のときは計算できません。「対象とする数値変数」ですから文字列は不可です。
数値のときでも計算できない場合があります。数値は必ずユニークでなければなりません。
外部変数の数値を降順にすると
「外部変数」の「ID」を降順へ変更するとどうなるのでしょうか。
dr サーモン サバ イカ サンマ 好き 苦手 嫌い まぐろ イクラ 海老 食べる khvar_ 1 1 0 0 0 1 0 0 1 1 0 0 12 2 1 0 1 0 0 1 0 1 1 0 0 11 3 0 0 0 0 0 0 1 1 1 1 0 10 4 1 0 0 0 0 0 0 0 1 0 0 9 5 0 1 0 0 1 0 1 1 1 0 0 8 6 0 0 0 0 1 0 0 1 0 1 0 7 7 0 1 1 0 1 1 0 0 0 1 0 6 8 0 0 0 0 0 0 0 1 0 0 0 5 9 0 0 0 0 0 0 0 1 0 0 1 4 10 0 0 1 0 1 0 0 1 0 0 1 3 11 0 1 0 1 0 0 0 0 0 0 0 2 12 1 1 0 1 0 1 0 0 0 0 0 1
もちろん「khvar_」は「ID」に合わせて降順になります。
プロットは全く同じですが色が逆転します。
・赤色の「サンマ」が青色へ
・青色の「イクラ」が赤色になりました。
これは計算結果であるPearson相関係数のプラスとマイナスが逆転したことを意味します。
昇順 khvar_ 降順 khvar_ サーモン -0.358464 0.358464 サバ 0.460882 -0.460882 イカ -0.027875 0.027875 サンマ 0.647750 -0.647750 好き -0.171379 0.171379 苦手 0.083624 -0.083624 嫌い -0.323875 0.323875 まぐろ -0.409673 0.409673 イクラ -0.856893 0.856893 海老 -0.195123 0.195123 食べる 0.388650 -0.388650 khvar_ 1.000000 1.000000
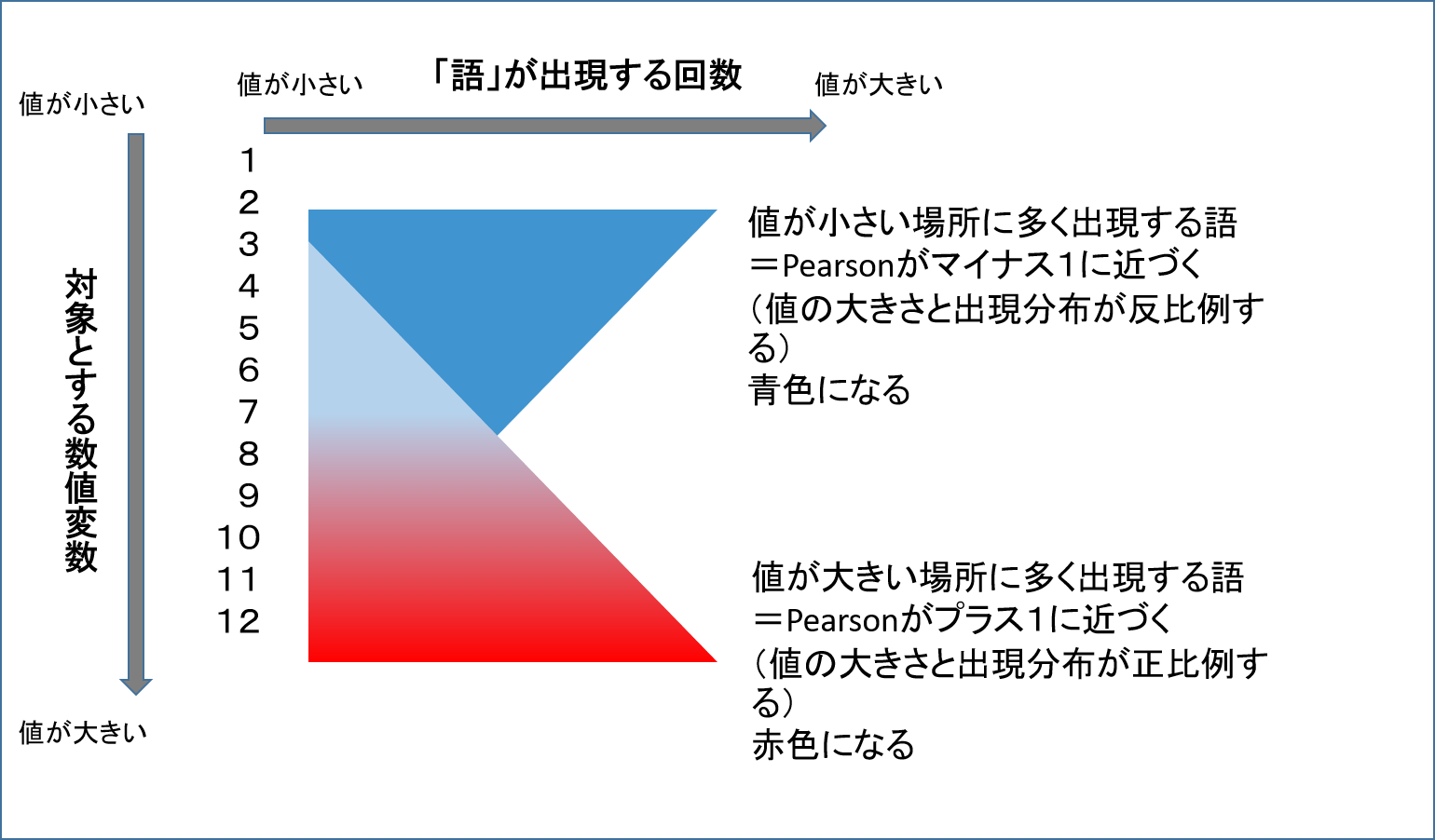
色相はPearson相関係数がプラス1に近づくほど赤く、マイナス1に近づくほど青くなります。
昇順のときプラス値が最も高いサンマが最も赤くなったのに対し、降順では最もマイナスになるから青くなります。
色(Pearson相関)が意味すること
Pearson相関係数
Pearson相関係数は「khvar_」と「語」が出現する回数との相関係数です。
① 「khvar_」の数値(値)が小さい、に対して「語」の出現回数が多い
一方の数値が小さく、一方の数値が大きいから負の相関(いわゆる反比例)になるからPearson相関係数はマイナス1に近づく。
② 「khvar_」の数値(値)が大きい、に対して「語」の出現回数が多い
一方の数値が大きくく、もう一方の数値も大きいから正の相関(いわゆる正比例)になるからPearson相関係数はプラス1に近づく。
色でわかること
・仮に「khvar_」=「出現位置」だとすると。
・プロットが青い「語」は分析対象テキストの前半に多く出現する「語」である。
・プロットが赤い「語」は分析対象テキストの後半に多く出現する「語」である。
・プロットが中間色の「語」は分析対象テキストの真ん中あたりに多く出現する「語」である。