重回帰分析(第２回)

投稿日: 2019年5月10日 2021年3月2日
投稿者: morita
カテゴリー: R, Tableau
タグ: 回帰分析

予測精度を上げる

都合が悪い店舗がある

店舗	売上高(万円)	面積(㎡)	駐車台数
A	2,500	45	4
B	800	40	3
C	1,500	40	4
D	1,700	45	5
E	1,800	50	7

＜新規出店予定地＞
店舗面積：40㎡
駐車台数：5台

　回帰分析においてＲ２値がおおむね予測精度をあらわします。新規出店予定地での売上高は単回帰分析、重回帰分析いずれの予測方法からも、新規店舗売上高予測は約1,500万円でした。

　Ｃ店舗の実績をみると
・店舗面積：40㎡
・駐車台数：4台
・売上高：1,500万円　ですから、
新規店舗の予測売上高1,500万円は妥当にみえます。

ところがＢ店舗はというと
・店舗面積：40㎡
・駐車台数：3台
・売上高：800万円　ですから、
　駐車台数が１台少ないだけで売上高が半分ほどです。逆に店舗Ａは面積が５㎡広いだけで2,500万円の売上高です。

都合が悪い店舗は除外

再掲

都合が悪い店舗
売れすぎ：店舗Ａ(見方によれば都合がいい)
売れなさすぎ：店舗Ｂ
この２店舗を除外します。

結果

左図から
式④　売上高 = 売上高 = 30*面積 + 316.667
新規店舗面積：40㎡　ですから
売上高 = 30＊40 + 316.667＝1,517万円
R-2 :0.964286

左図から
式⑤　売上高 = 92.8571*駐車台数 + 1171.43
新規店舗駐車台数：5台　ですから
売上高 = 92.8571＊5 + 1171.43＝1,636万円
R-2 :0.862245

＜結論＞
新規店舗予測売上高＝約1,600万円くらい
R-2も高い！

イレギュラー値を除外すればするほど、単純で美しい方程式を得ることができます。R-2もどんどんアップします。これが予測精度を上げる方法の一つです。

重回帰分析でも確認

Rコマンド（データは前回のものとおなじです）

#データの３行目から５行目（店舗Ｃ、Ｄ、Ｅ）を使います。
d2<;-d[3:5,]
#売上高を目的変数、面積と駐車場が説明変数です。
lm.2 <- lm(d2$売上高~.,data=d2[2:4])
#結果を表示します。
summary(lm.2)

＜結果＞

Call:
lm(formula = d2$売上高 ~ ., data = d2[2:4])

Residuals:
ALL 3 residuals are 0: no residual degrees of freedom!

Coefficients:
Estimate Std. Error t value Pr(<|t|)
(Intercept) -500 NA NA NA
面積 60 NA NA NA
駐車台数 -100 NA NA NA

Residual standard error: NaN on 0 degrees of freedom
Multiple R-squared: 1, Adjusted R-squared: NaN
F-statistic: NaN on 2 and 0 DF, p-value: NA

式⑥　売上高＝-500+60＊面積―100＊駐車台数
R-2=1
つまり式⑥で完全に説明できるという結果になります。

信頼区間95％を算出します。
Ｒコマンド

#lm.2の95％信頼区間を計算します。
pre.conf2 <- predict(lm.2, interval="confidence", level=0.95)
#結果を表示します。

#lm.2の95％信頼区間を計算します。
pre.conf2 &lt;- predict(lm.2, interval="confidence", level=0.95)
#結果を表示します。

＜結果＞

pre.conf2 ,<- predict(lm.2, interval="confidence", level=0.95)
警告メッセージ:
qt((1 - level)/2, df) で:   計算結果が NaN になりました
pre.conf2
fit lwr upr
3 1500 NaN NaN
4 1700 NaN NaN
5 1800 NaN NaN

完全一致しているので下限(lwr)、上限(upr)ともに「NaN」になります。

完全一致で予測してみる

式⑥　売上高＝-500+60＊面積―100＊駐車台数
店舗面積：40㎡
駐車台数：5台
新規店舗の情報を代入すると
売上高＝-500+60＊40―100＊5＝1,400万円

　完全一する方程式から算出した結果ですから間違いはありません。
　ただし分析対象として店舗Ａと店舗Ｂを除外しました。分析データにはＡ・Ｂ両店舗ともに「無い」のですが、店舗Ａと店舗Ｂは実在します。新規店舗を開店する場合、店舗Ｂのように売上高800万円になるリスクがなくなったわけではありません。

他にもデータがある

他のデータを加えてみる

　単回帰分析は１対１の関係です。説明変数は１個です。
　重回帰分析は１対多の関係をあらわすことができます。つまり、重回帰分析では説明変数になり得る複数のデータがあれば、それらのなかから最適なモデルを構築できる説明変数を採用できるということです。

　ここでは、面積、駐車台数に商圏単身者人口を加えて重回帰分析をおこないます。

Ｒで重回帰分析ふたたび

店舗	売上高	面積	駐車台数	商圏単身者人口
A	2,500	45	4	1,700
B	800	40	3	650
C	1,500	40	4	1,000
D	1,700	45	5	1,050
E	1,800	50	7	1,250

Rコマンド

d<-read.csv("ディレクトリ名/ファイル名.csv",header=T)
lm.3<- lm(d$売上高~.,data=d[2:5])
summary(lm.3)
pre3<-predict(lm.3)

＜結果＞

Call:
lm(formula = d$売上高 ~ ., data = d[2:5])

Residuals:
A B C D E
-15.24 -60.98 -15.24 167.68 -76.22

Coefficients:
Estimate Std. Error t value Pr(<|t|)
(Intercept) 721.3415 2290.1902 0.315 0.806
面積 -29.2073 75.2839 -0.388 0.764
駐車台数 81.2500 180.9712 0.449 0.731
商圏単身者人口 1.6372 0.3655 4.479 0.140

Residual standard error: 195.2 on 1 degrees of freedom
Multiple R-squared: 0.9745, Adjusted R-squared: 0.8978
F-statistic: 12.72 on 3 and 1 DF, p-value: 0.2026

pre3
1         2         3         4         5
2515.2439  860.9756 1515.2439 1532.3171 1876.2195

式⑦　売上高＝721.3415―29.2073＊面積＋81.2500＊駐車台数＋1.6372＊商圏単身者人口
R-2: 0.9745
「Residuals」の最大値も167.68です。

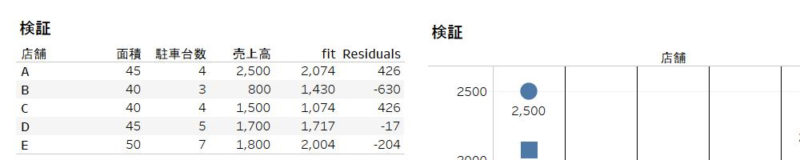
結果検証

fit

A	B	C	D	E
2515.2439	860.9756	1515.2439	1532.3171	1876.2195

Residuals:

A	B	C	D	E
-15.24	-60.98	-15.24	167.68	-76.22

いい感じですね。
＜新規出店予定地＞
店舗面積：40㎡
駐車台数：5台

　これに商圏単身者人口を加えて式⑦で計算するとより精度が高い結果を得ることができそうです。

＞重回帰分析(第１回)

morita

119