Pearson 相関　エクセル編

Pearson 相関　エクセル編

エクセルのアドイン機能「相関」を使用してPearson相関係数を算出、ピボットグラフでビジュアル化する手順を解説しています。

分析ツールをアドインして計算

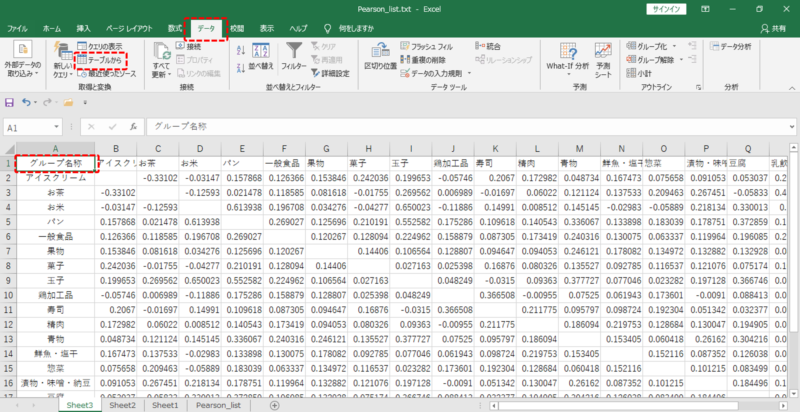
データについて
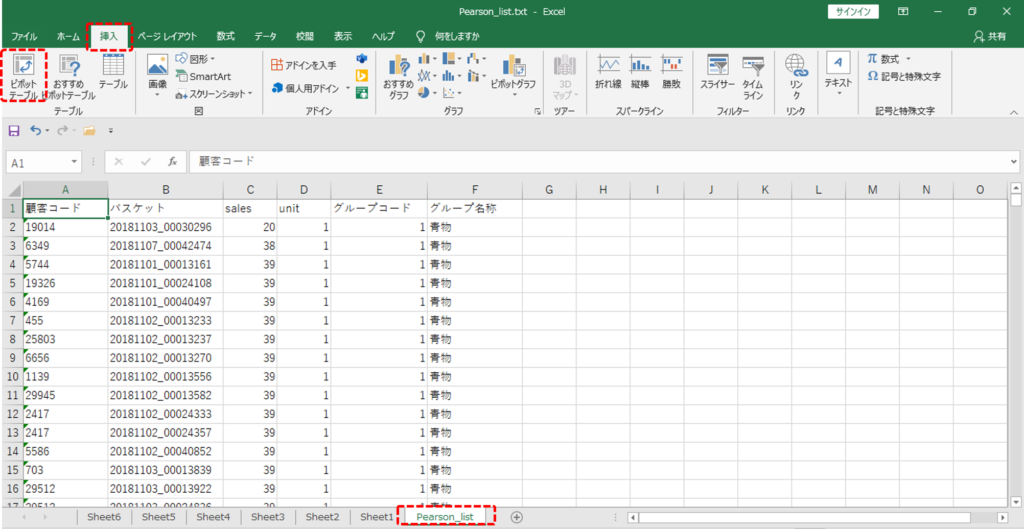
顧客コード,バスケット,sales,unit,グループコード,グループ名称
19014 ,20181103_00030296,20,1,1,青物
6349 ,20181107_00042474,38,1,1,青物
5744 ,20181101_00013161,39,1,1,青物
19326 ,20181101_00024108,39,1,1,青物
4169 ,20181101_00040497,39,1,1,青物
455 ,20181102_00013233,39,1,1,青物

＞トレーニング用データはこちら

総行数：93,760（ヘッダー行を含む）
バスケット数：20,653
顧客コード数：4,301
グループ名称数：20
sales合計：37,354,518
unit合計：201,912

データの構造
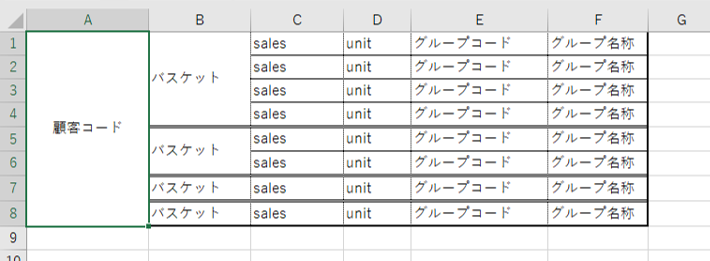
最小集計粒度は「バスケット」
「顧客コード」でも集計できます。
テキストファイルをエクセルへ変換
＞テキストファイルへエクセルへ変換する方法はこちら

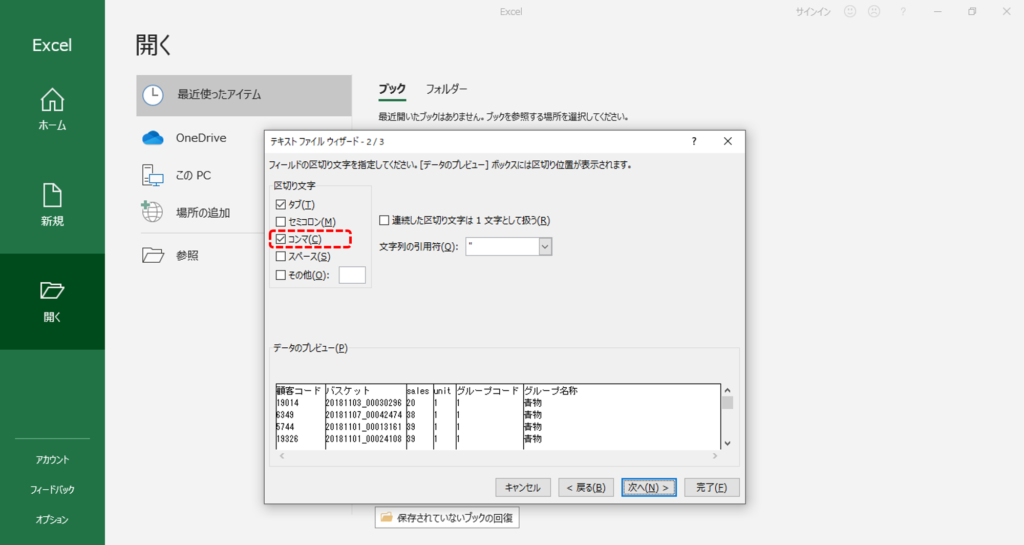
・「区切り文字」は「コンマ」です。

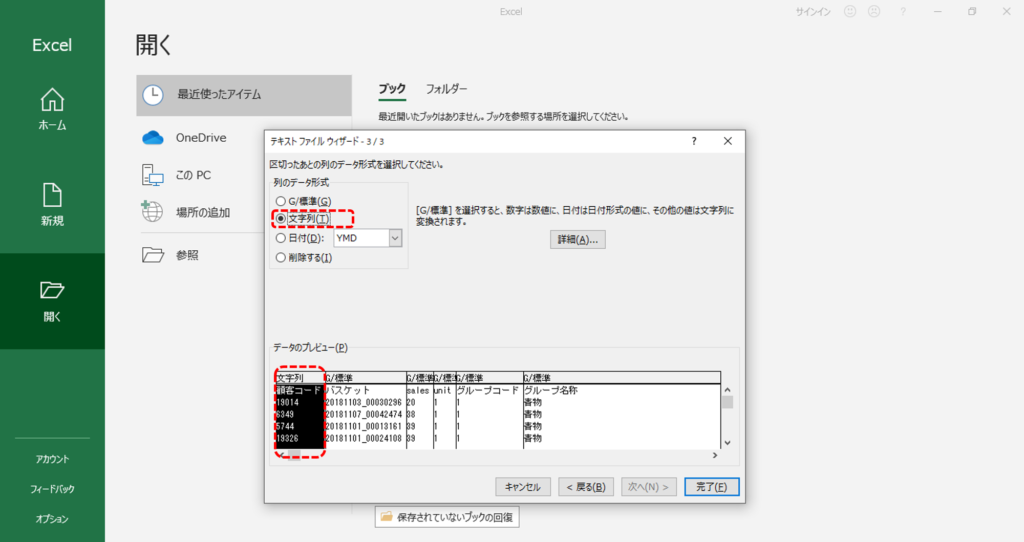
変換する列を選択して、列の表示形式のラジオボタンをクリックします。

・「顧客コード」は「文字列」です。（念のため）

ピボット
「グループ名称」を列へピボットします。

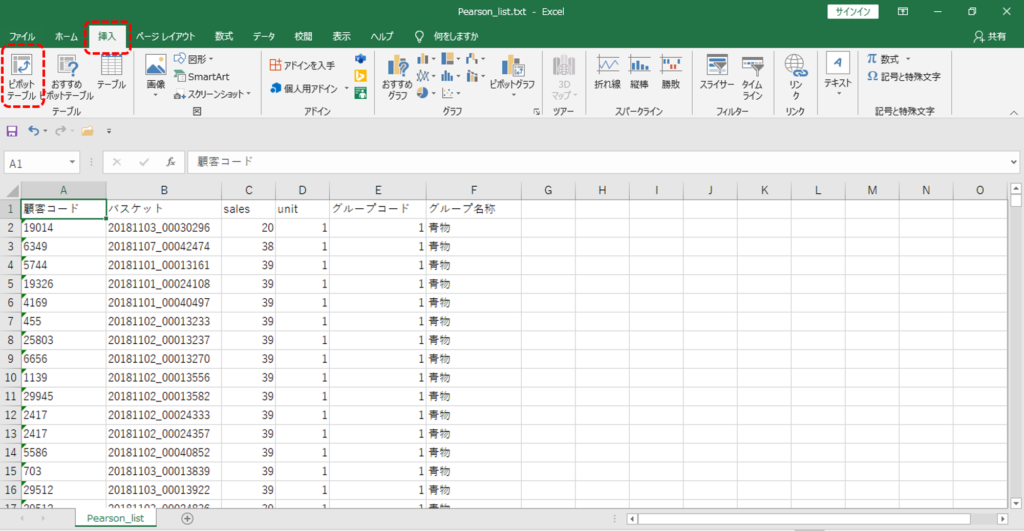
・「挿入」タブ
・「ピボットテーブル」を選択します。

値は「sales」です、数量のときは「unit」に設定します。

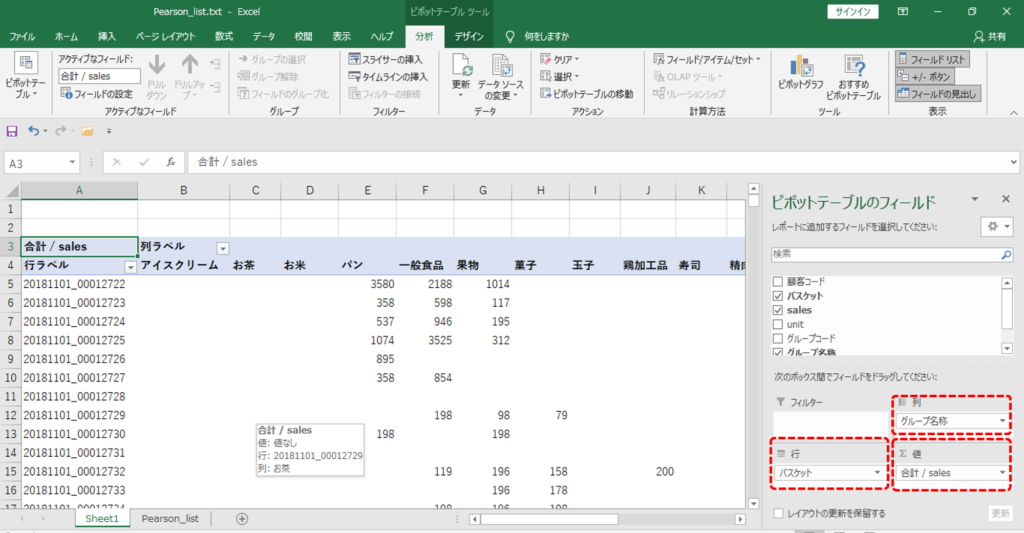
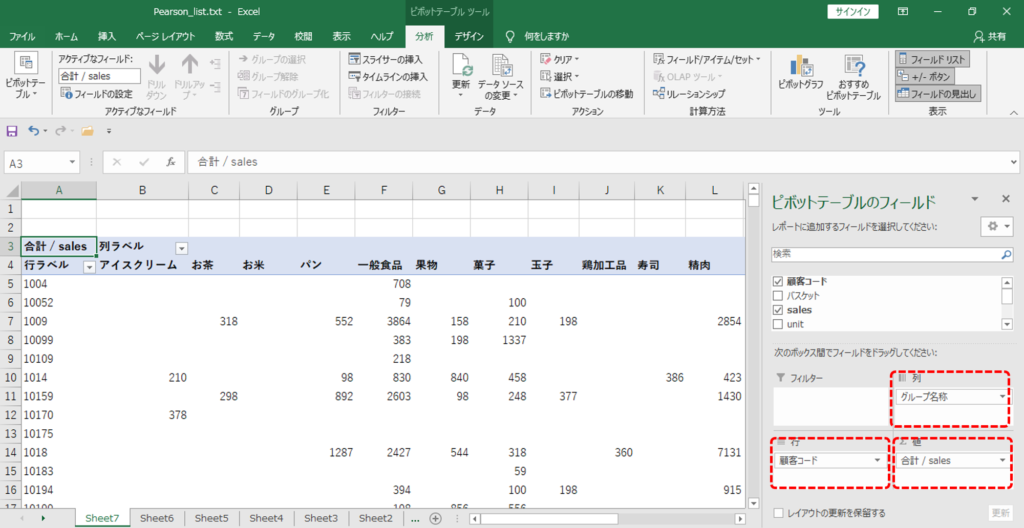
・「行」＝「バスケット」
・「列」＝「グループ名称」
・「値」＝「sales」

列名「総計」を右クリックします。

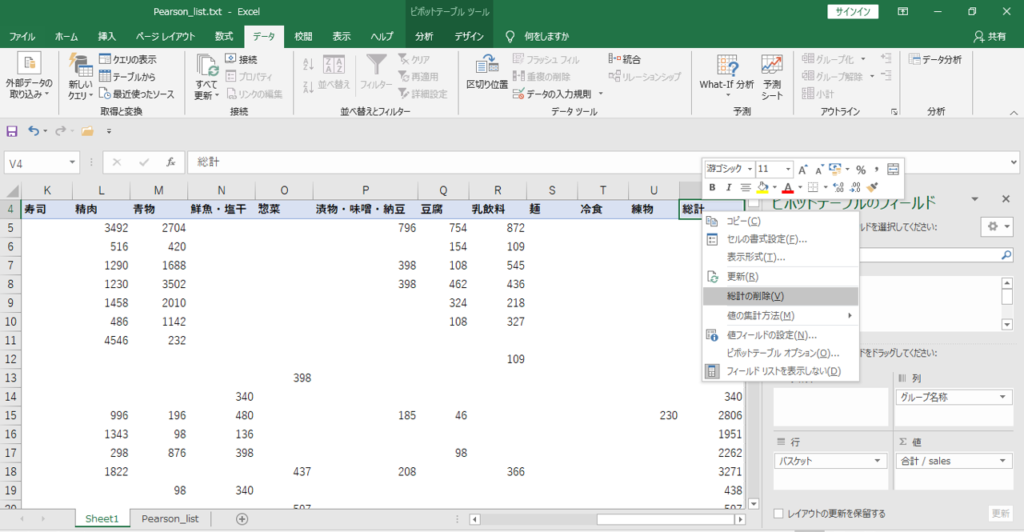
横計・縦計の総計を削除します。

分析ツールをアドイン
「その他」をクリックします。

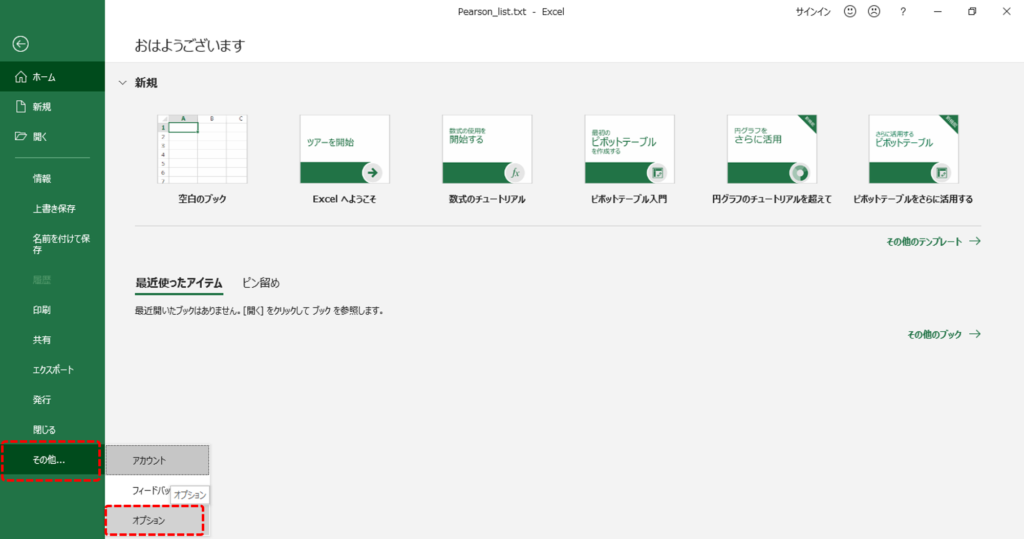
「ファイル」タブからホーム画面へすすみます。
・「その他」をクリックし「オプション」を選択します。

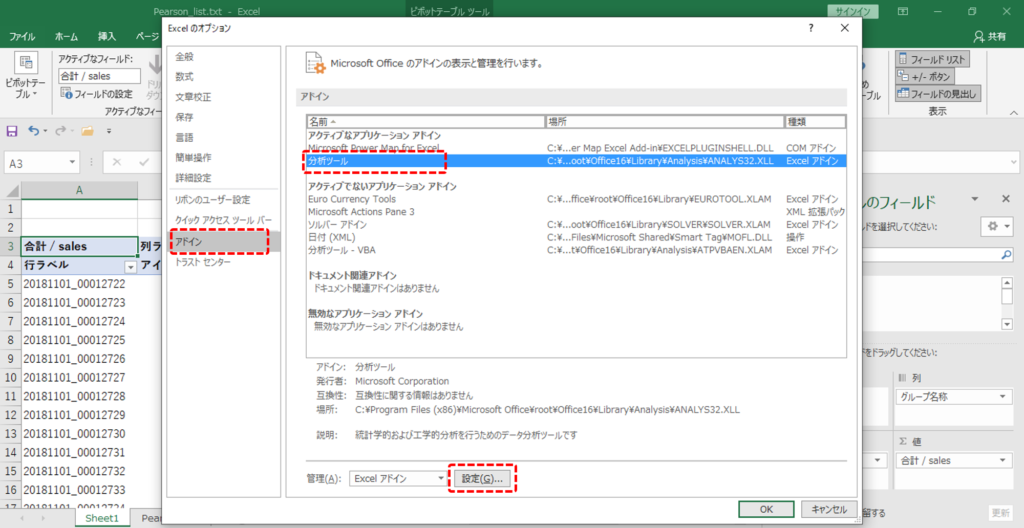
PC内のフォルダーにあるのでネットに繋がっていなくても大丈夫そうです。

・左側のメニューから「アドイン」を選択
・「分析ツール」→「設定」の順にクリックします。

前の手順で「設定」をクリックすると開きます。

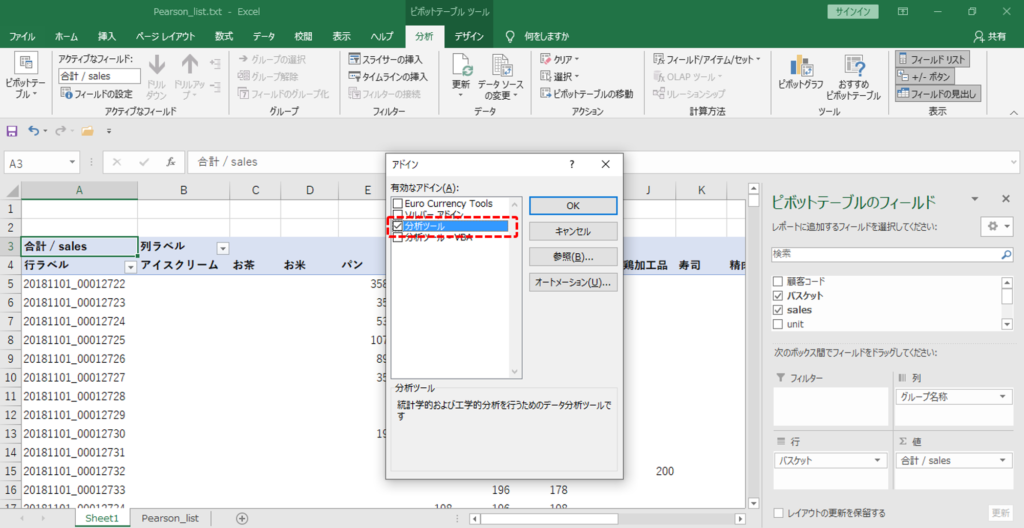
窓が開いたら
・「分析ツール」をチェックして「OK」

Pearson相関係数を計算

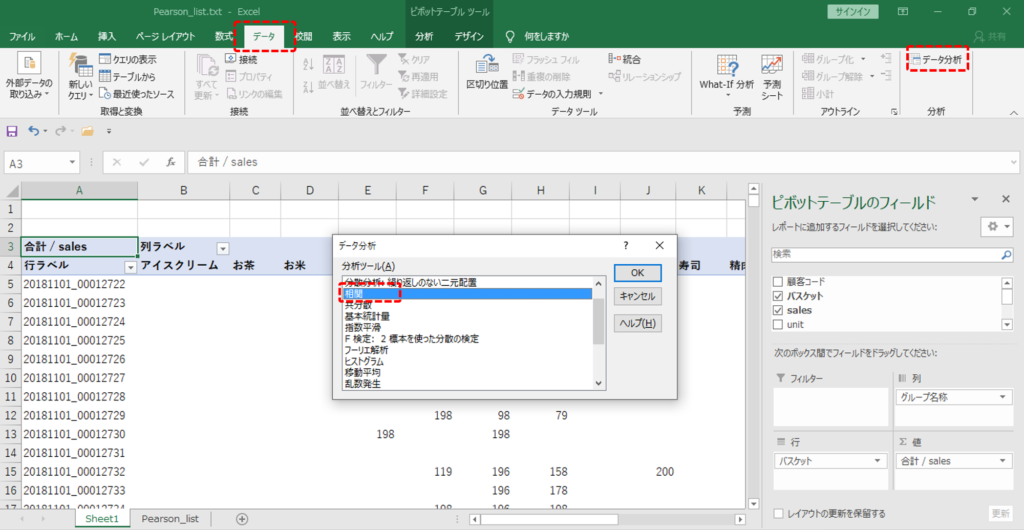
・「データ」タブ→「データ分析」
・「相関」を選択します。

「入力範囲」をうまく設定してください。

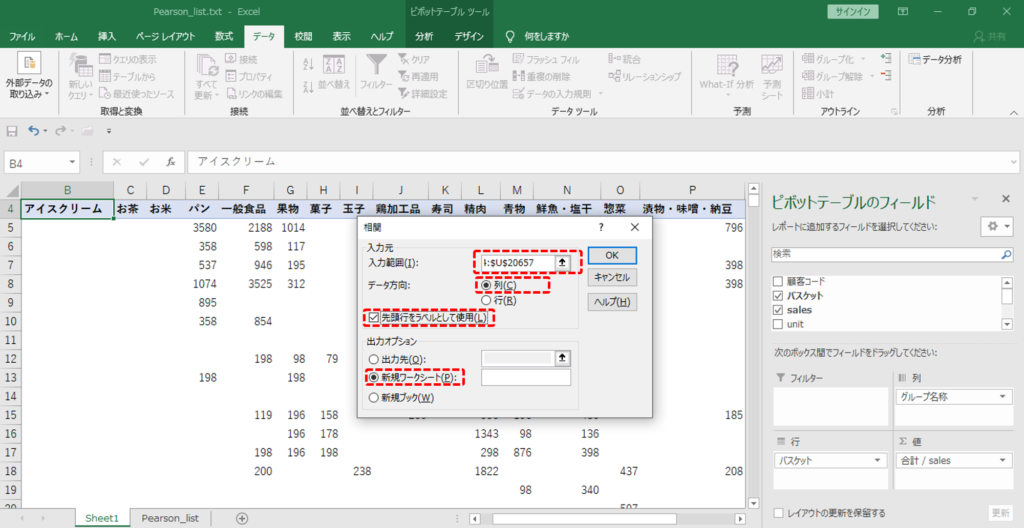
・入力範囲を設定します。
　ピボットテーブルの左端列（バスケット列）を除くすべてのデータ範囲です。総計列・総計行が残っているときは、入力範囲から除外してください。

・「データ方向」＝「列」
・「先頭行をラベルとして使用する」へチェック
・「新規ワークシート」へ出力しましょう。

対角線上の値は「１」になります。

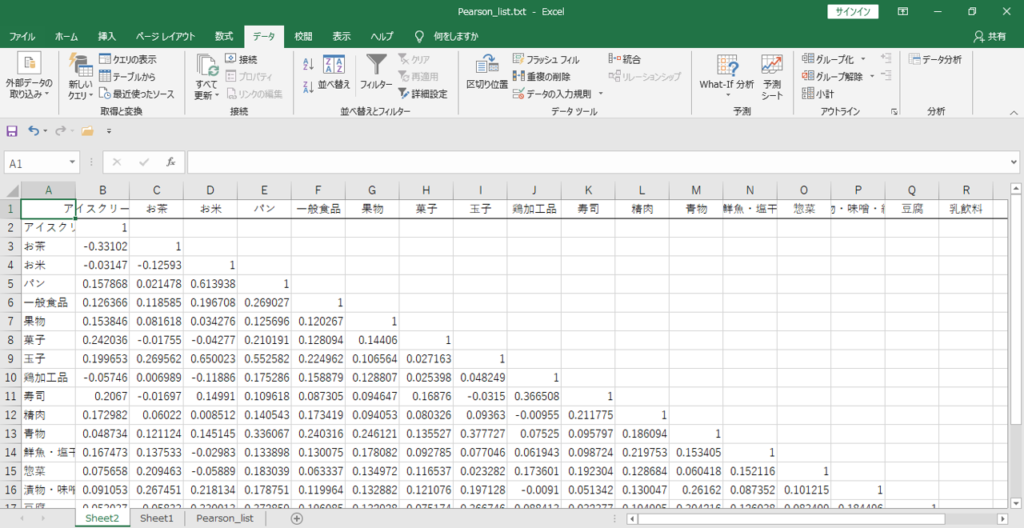
クロス集計表の下三角形へ数値が出力されれば完成です。

結果をビジュアル化する

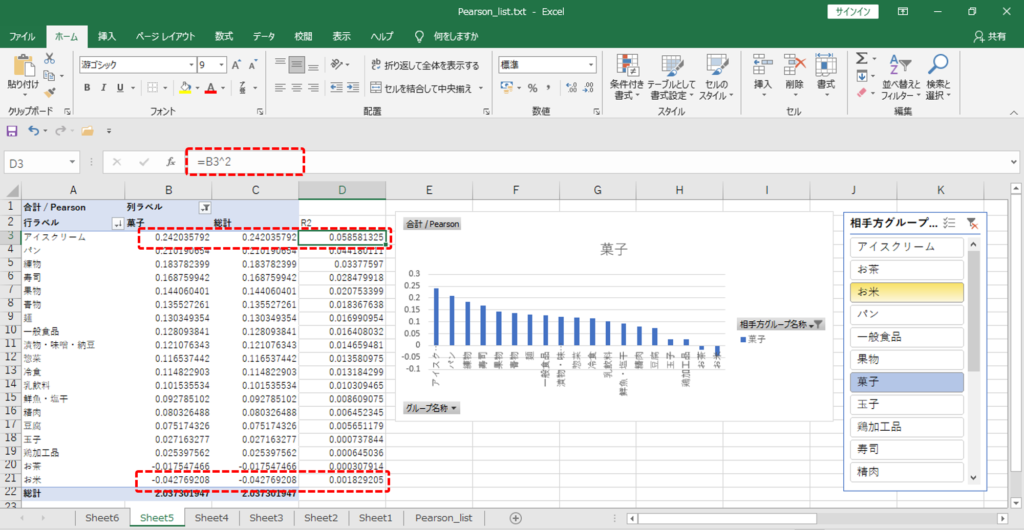
列指向形式へ変換
表の部分だけをコピーします。シート全体をコピーすると失敗します。

表をコピーします。

セルを右クリック、「形式を選択して貼り付け」を選択します。

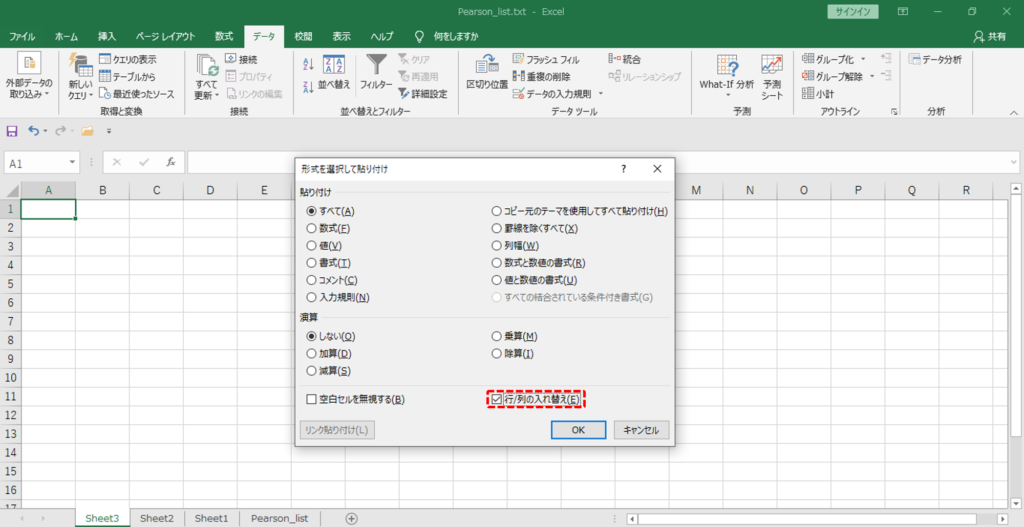
あたらしいシートへ
・行列を入れ替えてペーストします。

コピー元のシートから値を引っ張てきます。

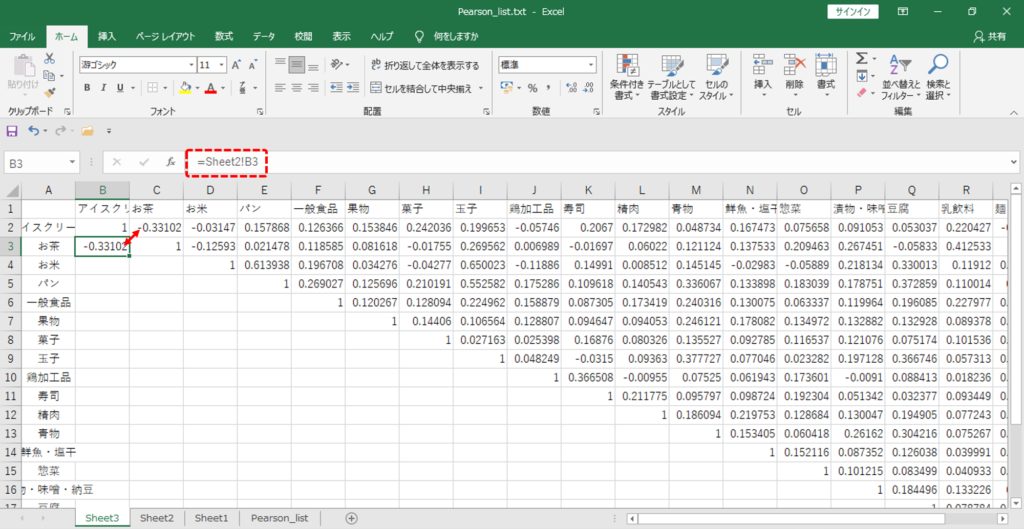
空欄へコピーもとの値を入れこみます。
画像のように「値１」をはさんで対角線上に同一値が入ります。

対角線上の「１」をはさんで同一値になるはずです。

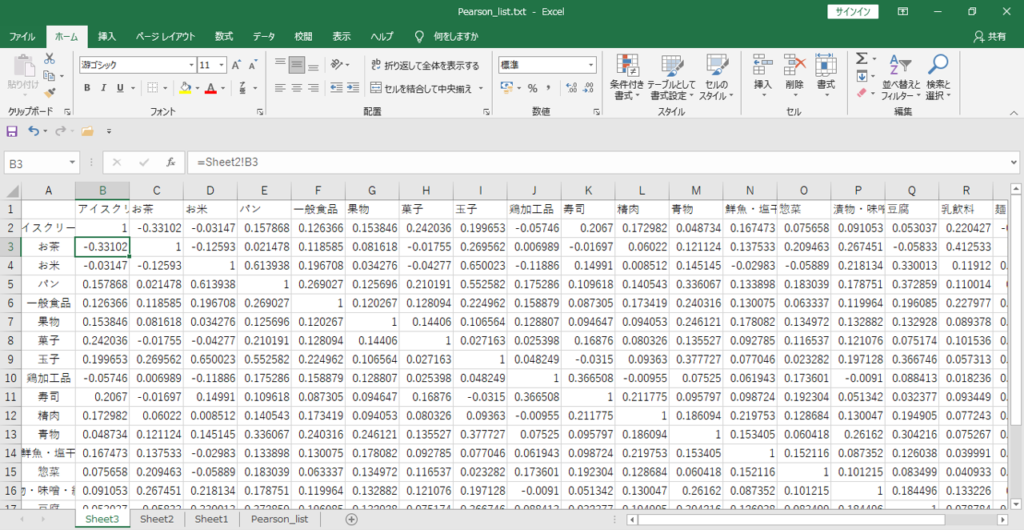
すべてのセルを値で埋めます。

対角線上の値「１」を消します。

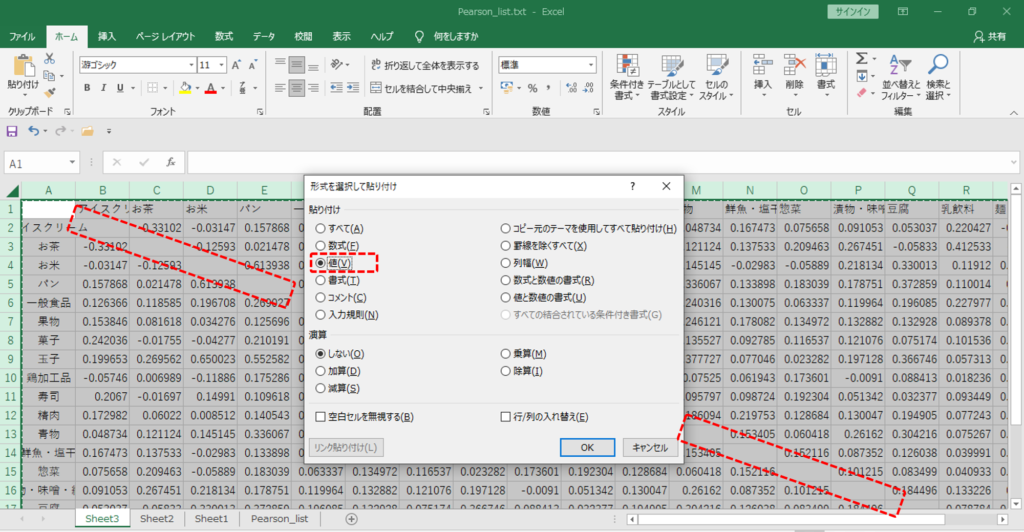
・対角線上の「値１」をデリートします。
・念のため、すべての値を値貼り付けします。

A１セルが空欄になっていると思います。

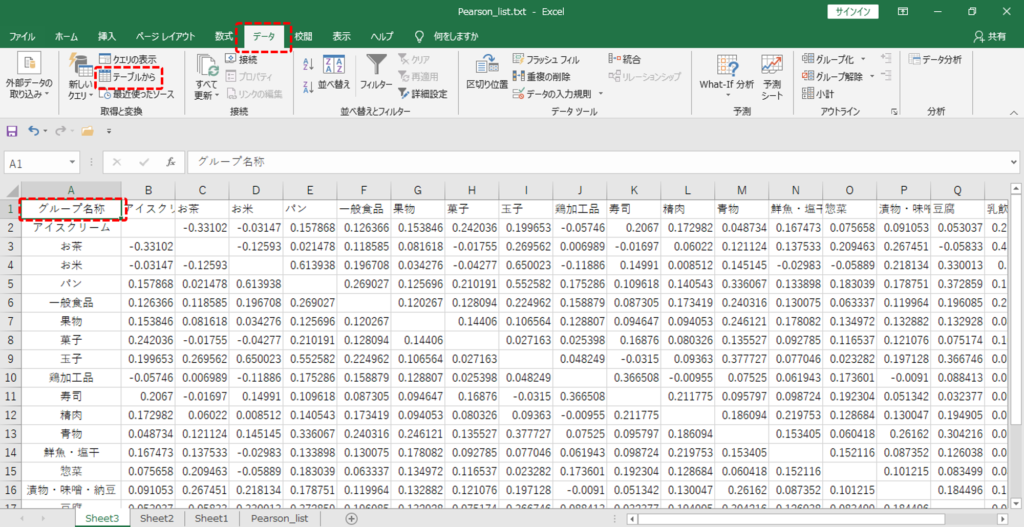
・A列名を「グループ名称」にします。
・「データ」タブ→「テーブルから」をクリックします。

列から行へピボットします。

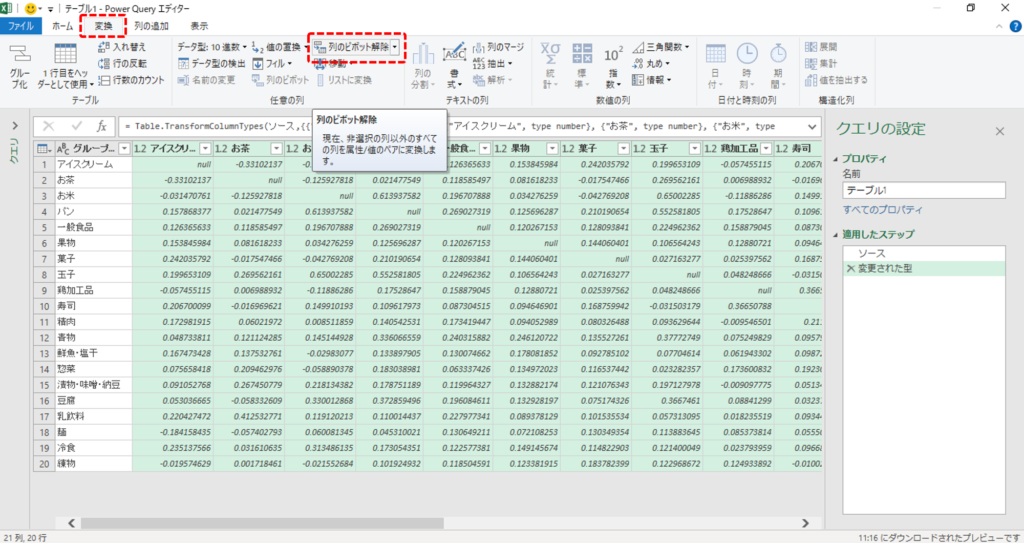
Power Query エディターが開きます。
・「グループ名称」の列を除くすべての列を選択
・「変換」タブ→「列のピボット解除」をクリックします。

列名をダブルクリックするか、右クリックします。

列名を変更します。

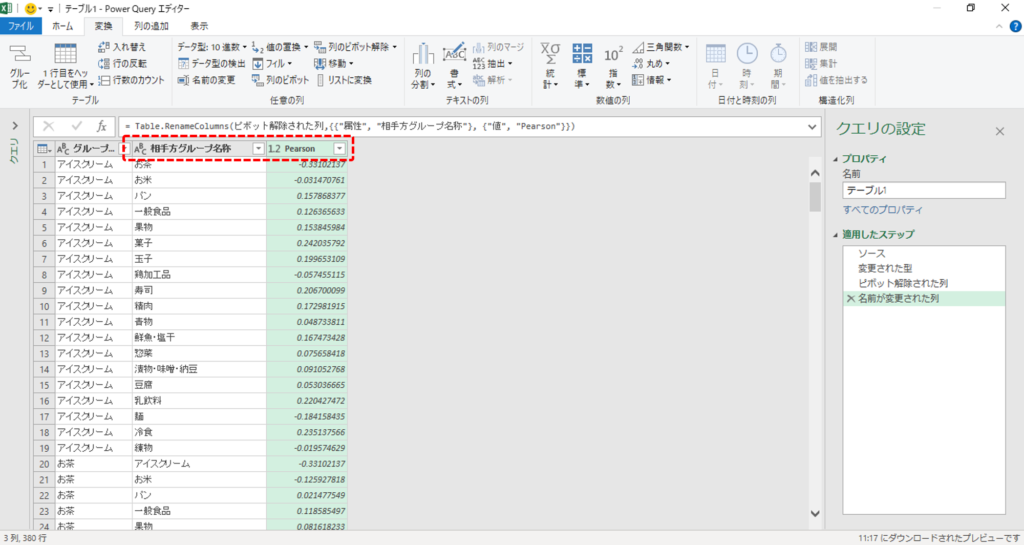
「×」をクリックすると窓が開くので「閉じて読み込む」でもOKです。

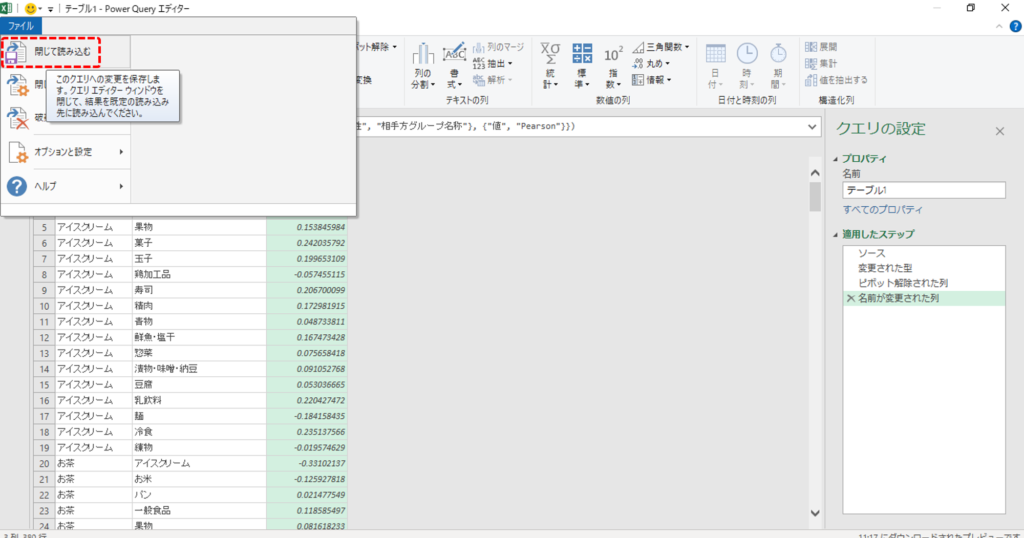
・「ファイル」タブ→「閉じて読み込む」

ピボットグラフ
A1へカーソルを合わせます。

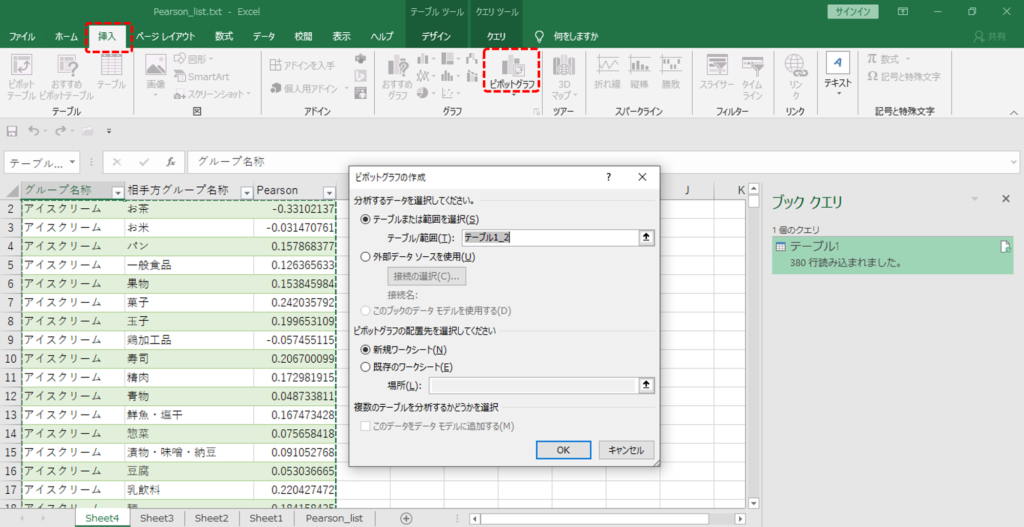
列指向形式へ変換できたら
・「挿入」タブ→「ピボットグラフ」

右側に表示されている「ブッククエリ」は「×」で非表示にできます。

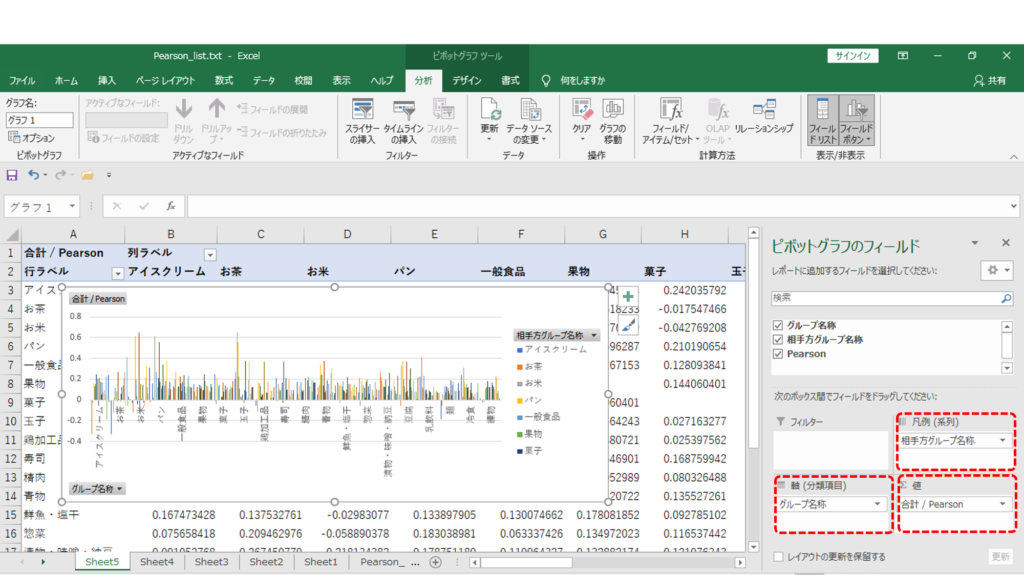
・「行」＝グループ名称
・「列」＝相手方グループ名称
・「値」＝Pearson

スライサーは「分析」タブにあります。

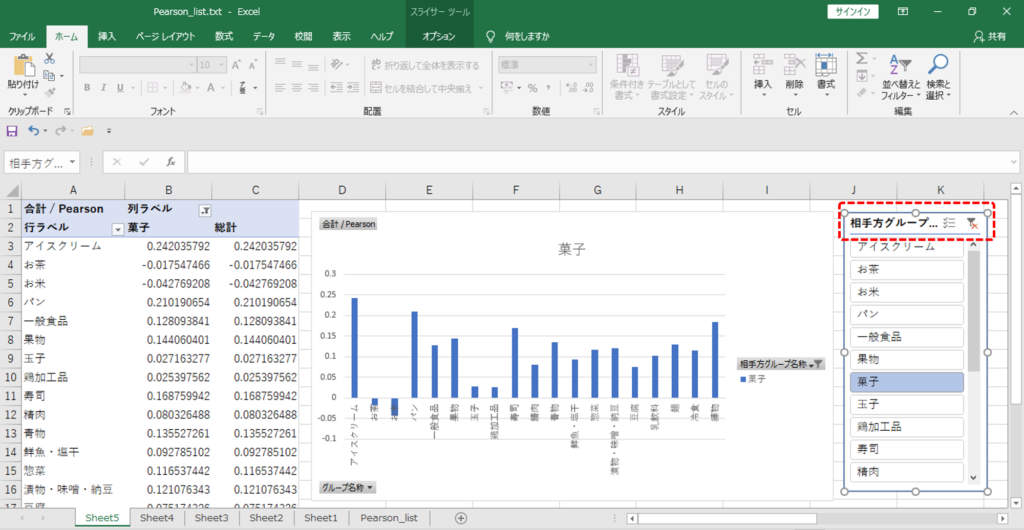
・「スライサー」＝「相手方グループ名称」

並び替えをしたい列の値へカーソルを合わせて右クリックします。

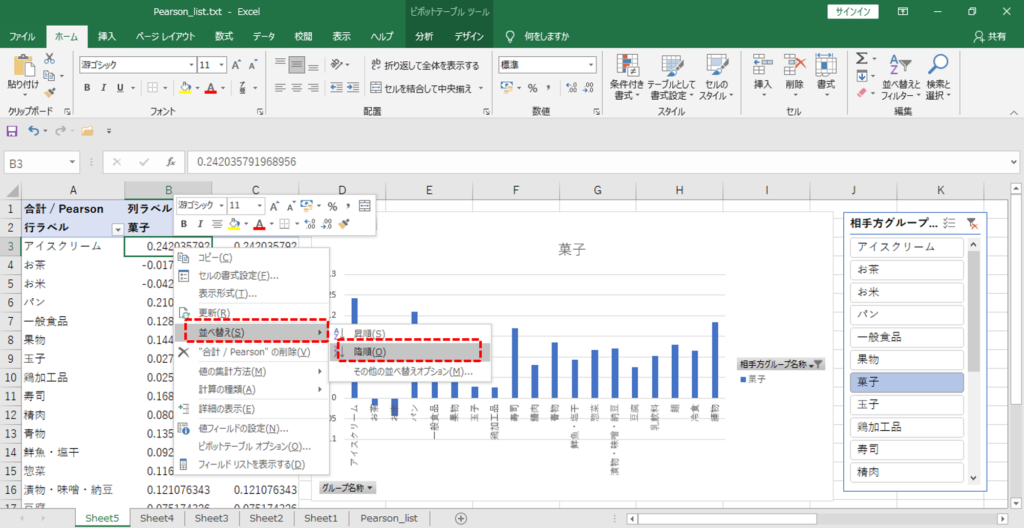
・値（Pearson）を降順に並び替えます。

スライサーを操作することでグループ名称を変更できます。

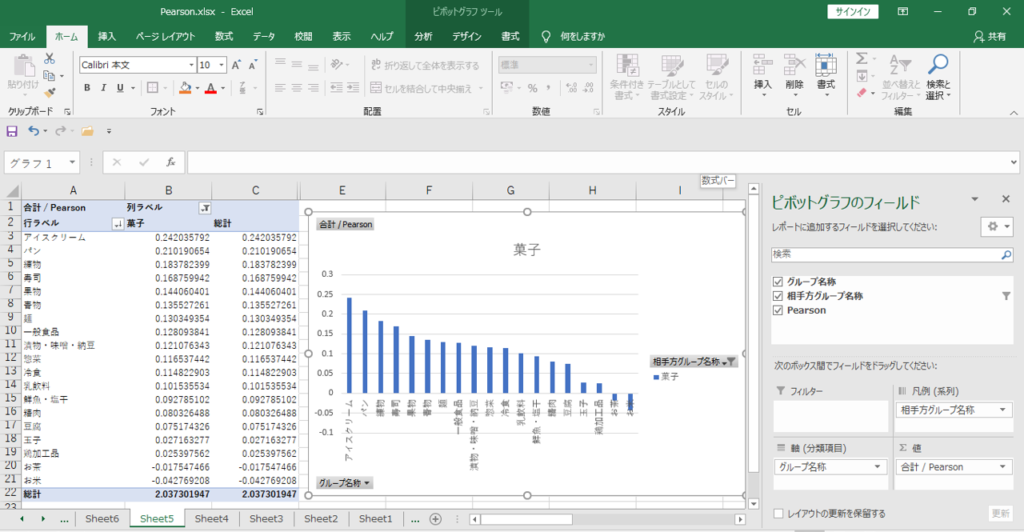
これで完成です。

検証

散布図作成
A列はコピー不要です。

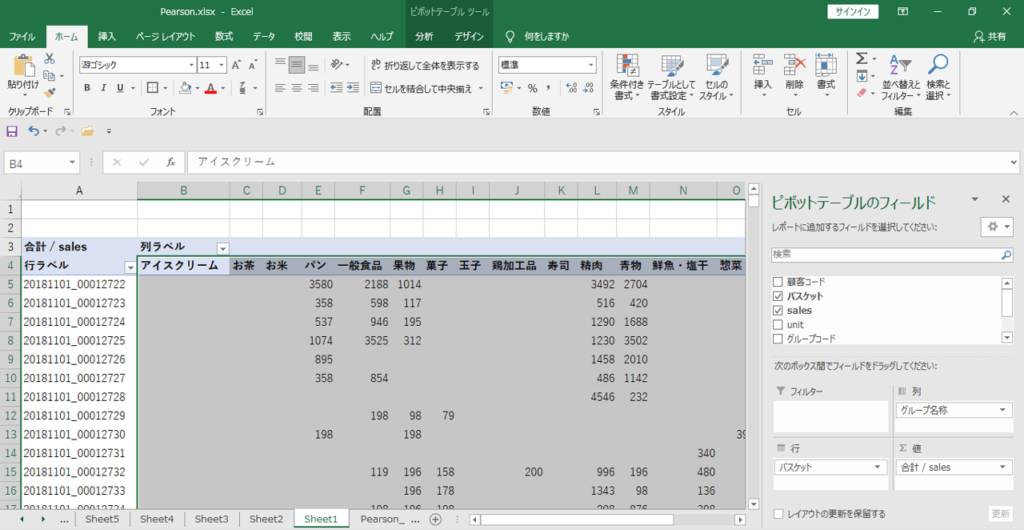
　はじめに作成したピボットテーブルへ戻ります。バスケットごとにsalesを集計したピボットテーブルです。

・バスケットの列、縦総計・横総計を除く全体をコピーします。

ピボットテーブルの状態で散布図を描こうとしたらできないみたいです。何か方法があるのかどうか・・・

・あらたしいシートへペーストします。

エクセルで散布図を描く方法は、これがいちばん簡易なのかどうか・・・

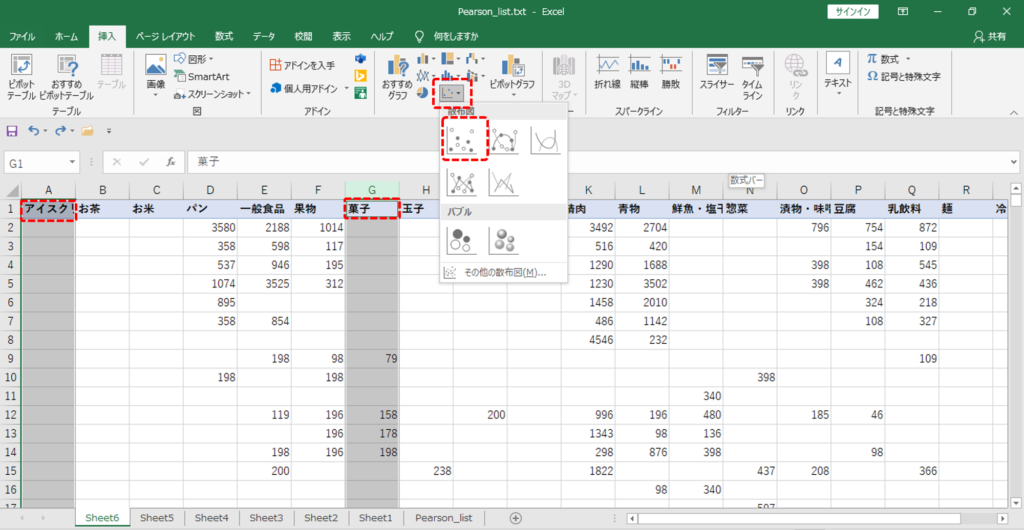
・２列を選択します。（例：「菓子」「アイスクリーム」）
・「挿入」タブ→「散布図」をクリックします。

近似曲線は「線形」です。

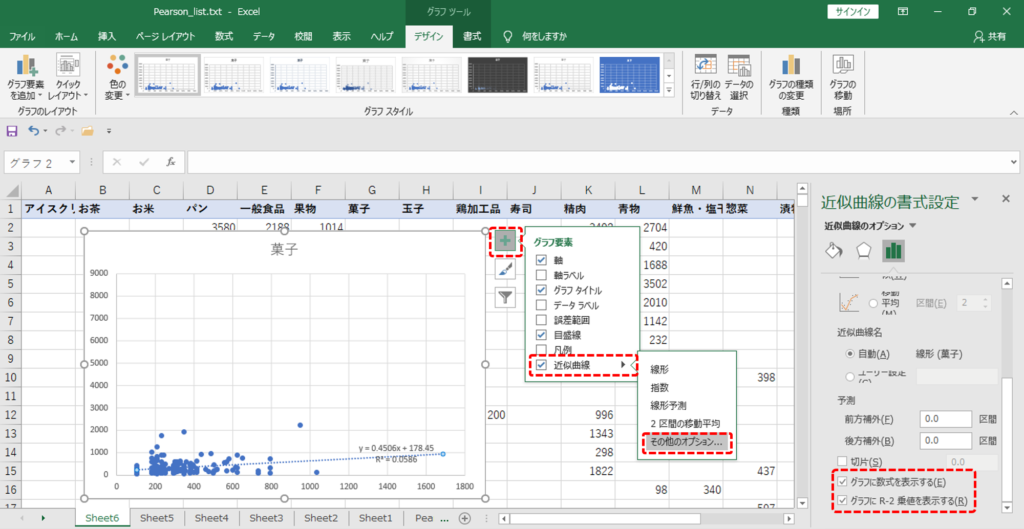
・＋マークをクリック
・「近似直線」へチェック
・「その他オプション」→「グラフに数式を表示する」「グラフにR-2乗値を表示する」をチェックします。

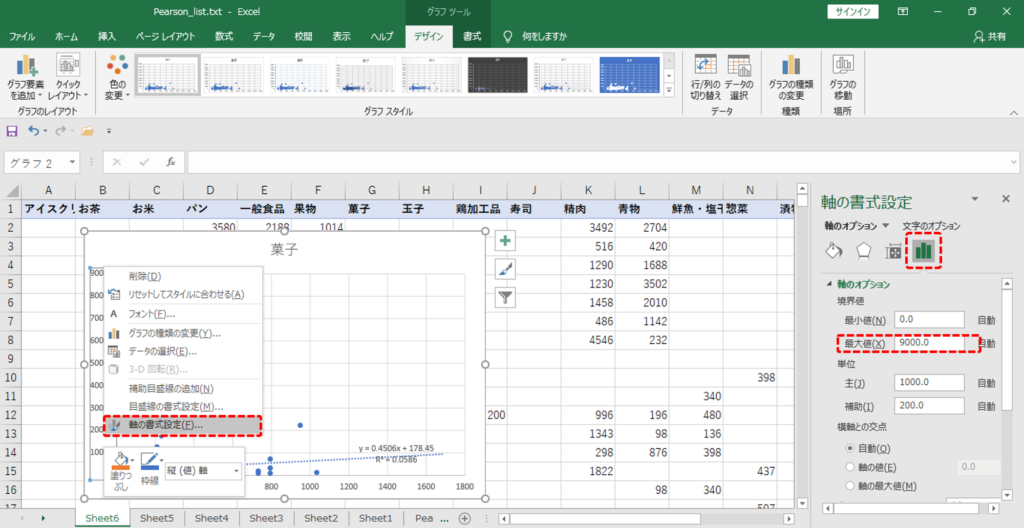
R-2乗値を確認できればそれでよいのですが、散布図を見やすくしておきます。

・縦軸のスケールを右クリック
・最大値を入力して見やすくします。

近似線が右肩下がりになる散布図もあります。

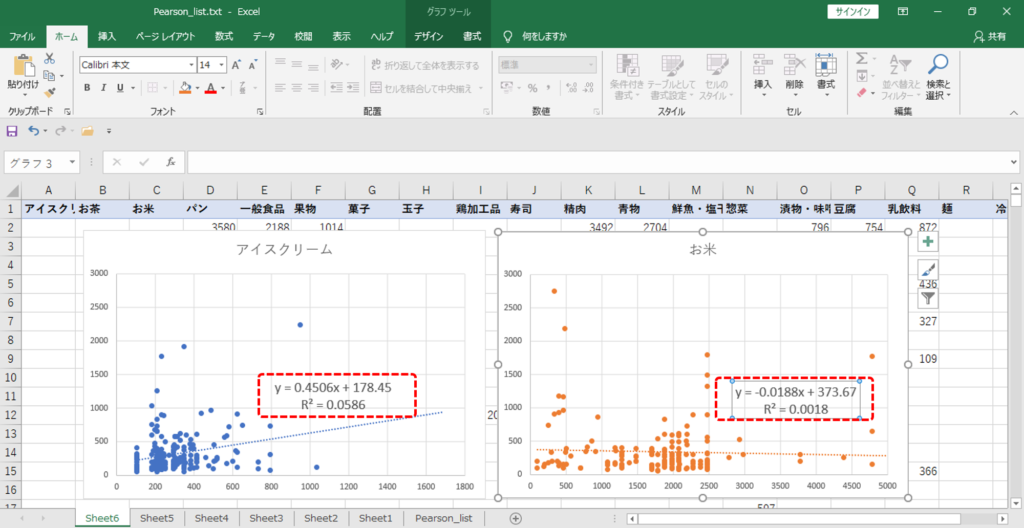
・R2の値を確認しましょう。

R-2乗値はつねに正の値になりますが、Pearson相関係数は近似線が右肩下がりのとき、マイナス値になります。

R2=Pearsonの2乗です。

顧客コードで集計すると結果は違う
テキストファイルを変換したシートへ戻ります。

もとデータです。

列が「顧客コード」です。

・「顧客コード」で集計します。

ピボット後の手順は「バスケット」集計と同一です。

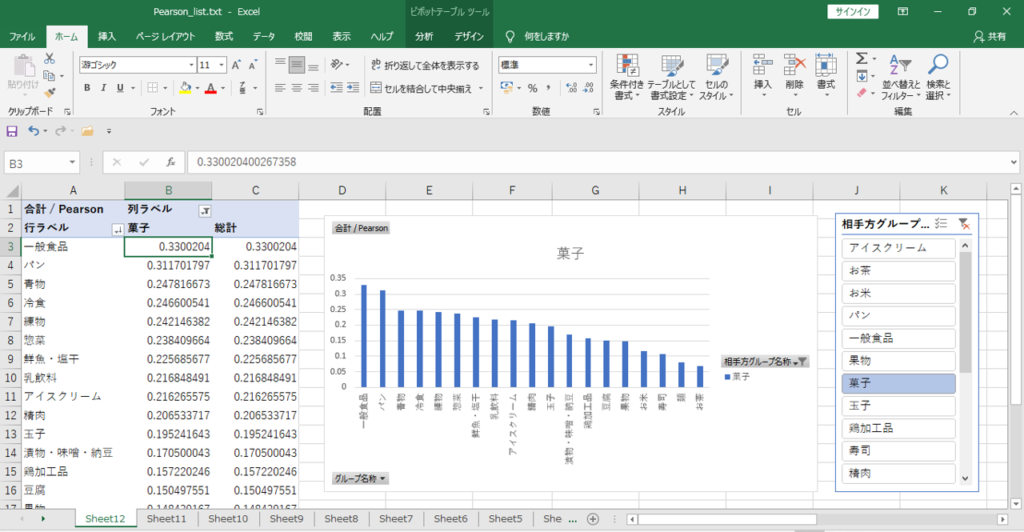
バスケットと同様の手順で棒グラフを作成します。

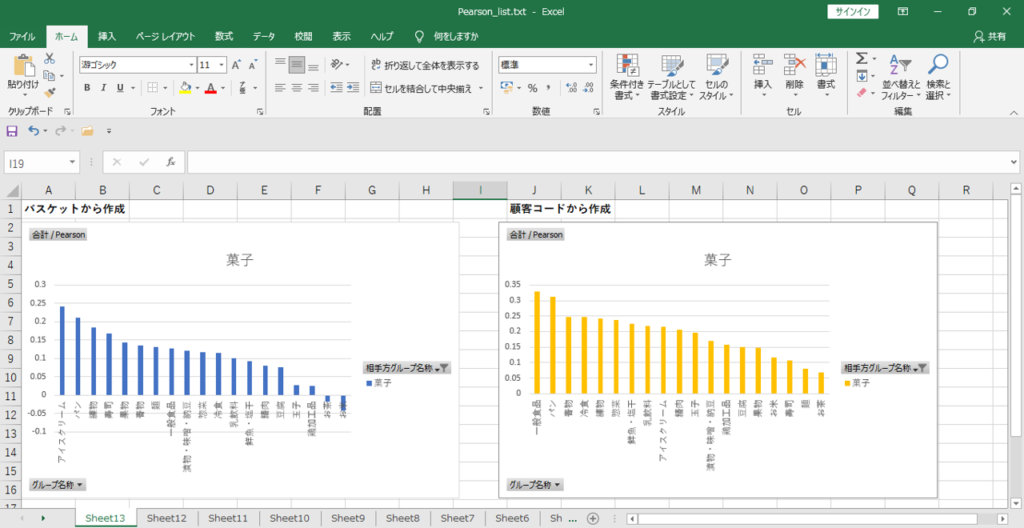
集計粒度が粗い「顧客コード」から算出したPearson相関係数の方が一般的には大きくなります。

バスケットから計算したPearsonと顧客コードから計算したPearsonを比較すると違いがあります。

バスケットと顧客コードの違い
サンプルデータの構造

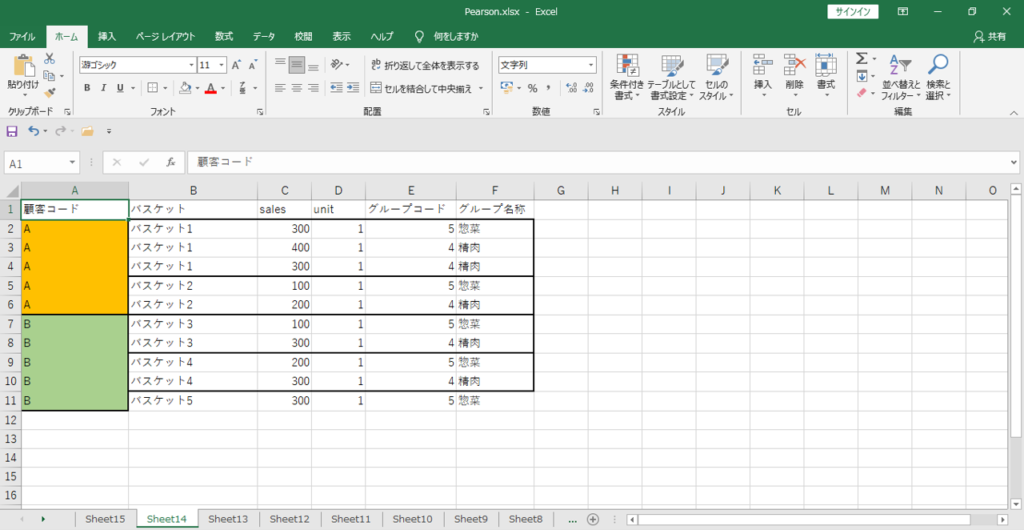
画像のようなデータがあるとします。

・バスケットのユニークカウント数＝５
・顧客コードのユニークカウント数＝２

バスケットで集計するとデータポイント数は４です。

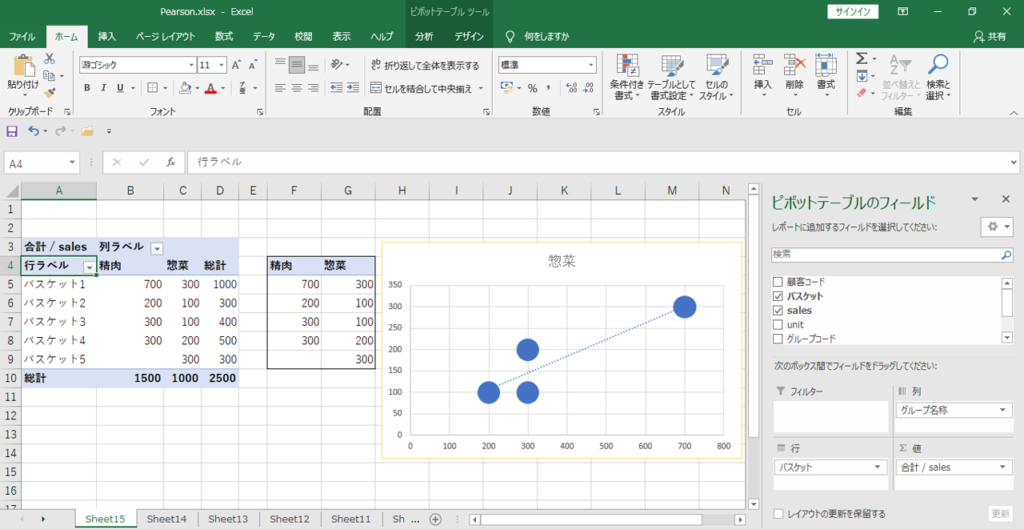
バスケットを集計レベルとして散布図を作成すると、
「精肉」と「惣菜」の両方が入っているバスケット数は４です。

したがって散布図へプロットされるデータ点の数は４です。

顧客コードで集計するとデータポイント数は２です。

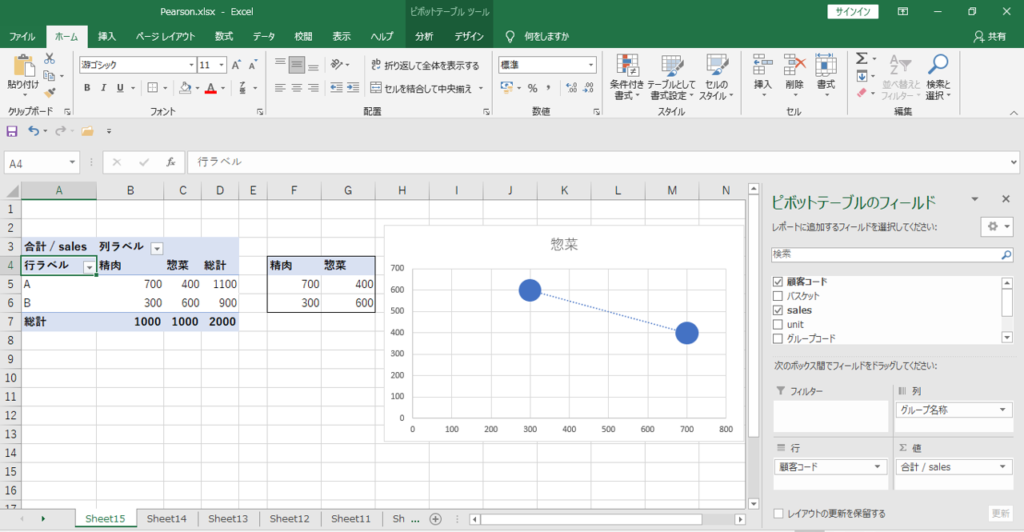
顧客コードを集計レベルとして散布図を作成すると、
「精肉」と「惣菜」の両方が入っている顧客コード数は２です。

したがって散布図へプロットされるデータ点の数は２です。

計算のもとになる散布図（相関図）が違うから相関係数も違うということです。

119