テキストマイニングの基本機能「関連語検索」、Jaccard、確率差などの各種係数の解説も。

テキストマイニングツール「KHcoder」の活用メモ
開発者である樋口先生に感謝！
【今回の分析対象テキストはこちらからコピーできます】

関連語検索

関連語検索

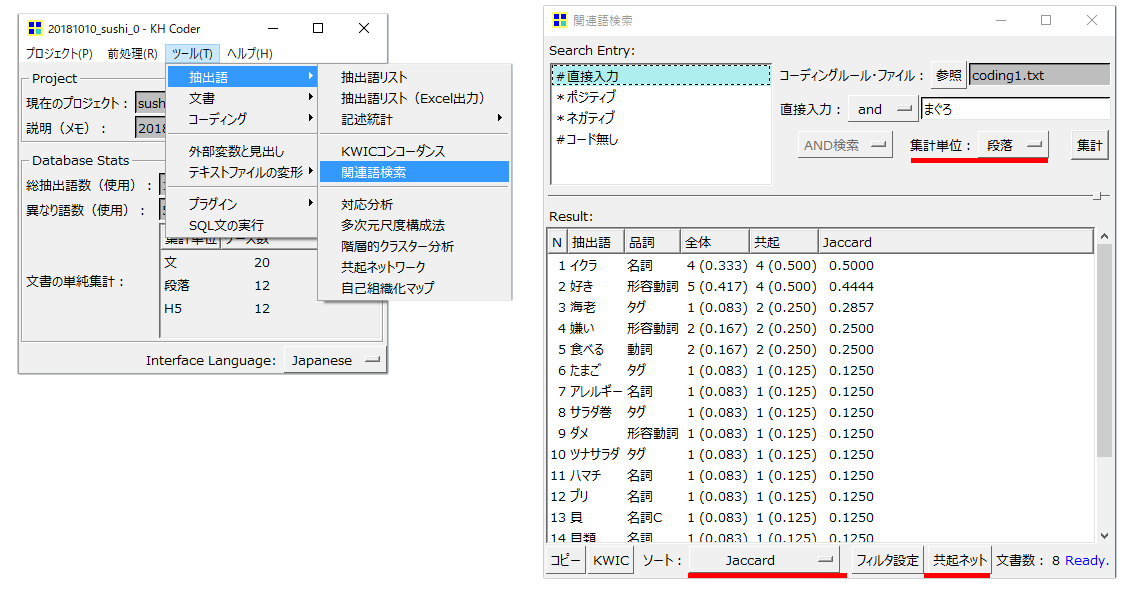
・「抽出語」→「関連語検索」をクリックするとウインドウが開きます。
・「Search Entery」の「＃直接入力」をクリックします。
　「＃直接入力」は検索したい「語」を入力する機能です。

・「集計単位」を「段落」に設定します。
　今回は「分析対象テキスト」のなかで最多頻出語「まぐろ」で説明します。

　関連語検索機能はまるで検索機能のように思いがちですが、これは分析機能です。分析ですから、以降は分析結果を解説します。

　集計単位を段落に設定しました。
・「抽出語」の右側に表示される「全体」と「共起」の数値 (整数) は「抽出語」が出現する「段」数です (今回は集計単位を「段落」に設定したから) 。
・集計単位を「文」に設定すると「文」数になります。

　関連語検索結果は集計単位の設定によって「Ｈ５」「段」「文」それぞれで違う結果になります。はじめの集計単位設定がまずは重要です。

　表示数値は決して「語」が出現する回数ではありません。

　２行目の「好き」を例に解説します。 (表記揺れの吸収のところで投稿したとおり、「イクラ」と「海老」の段数が実際とは違うことをあらかじめご了承ください)

表示される「語」、隠れている「語」

関連がある＝共起している　これがポイントです。

　「関連語検索」ですから、はじめに窓へ入力した「まぐろ」と関連する「語」だけが表示されます。「分析対象テキスト」全体には３８の異なり使用語があります。「まぐろ」と入力すると、１９「語」が表示されます。

　出現する全語のうち「半分がまぐろと関連があるのだろう」と、想像ができます。

　実は、関連があるのに表されない「語」が存在しています。通常、出力結果にはデフォルトでフィルターが設定されているからです。

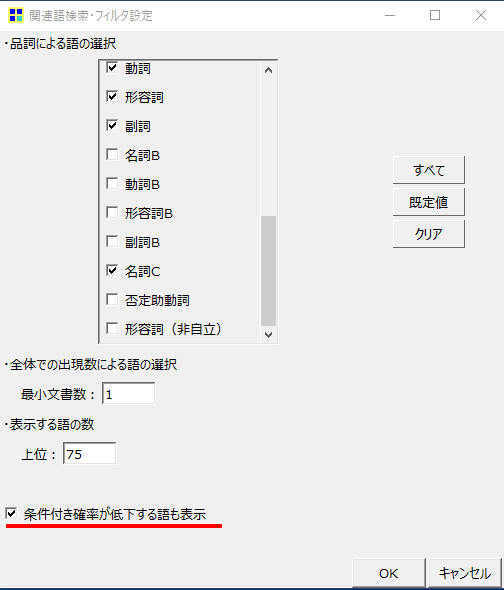
・「フィルター設定」をクリックするとウインドウが開きます。
・「品詞」のフィルターは今回の「分析対象テキスト」では重要ではないのでそのままにしておきます。
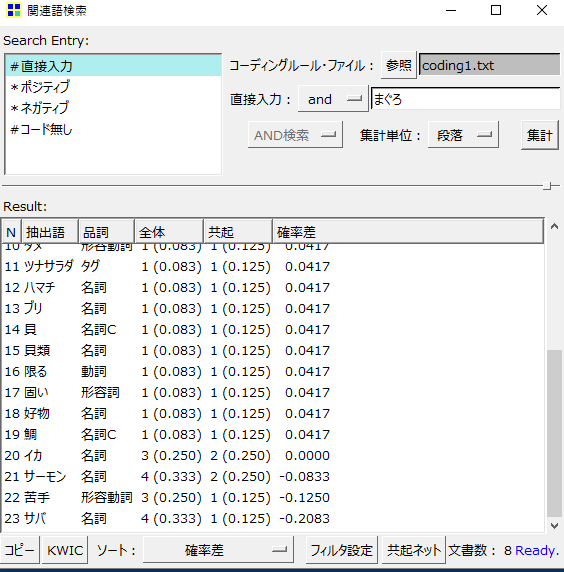
・下の「条件付き確率が低下する語も表示」をクリックします。

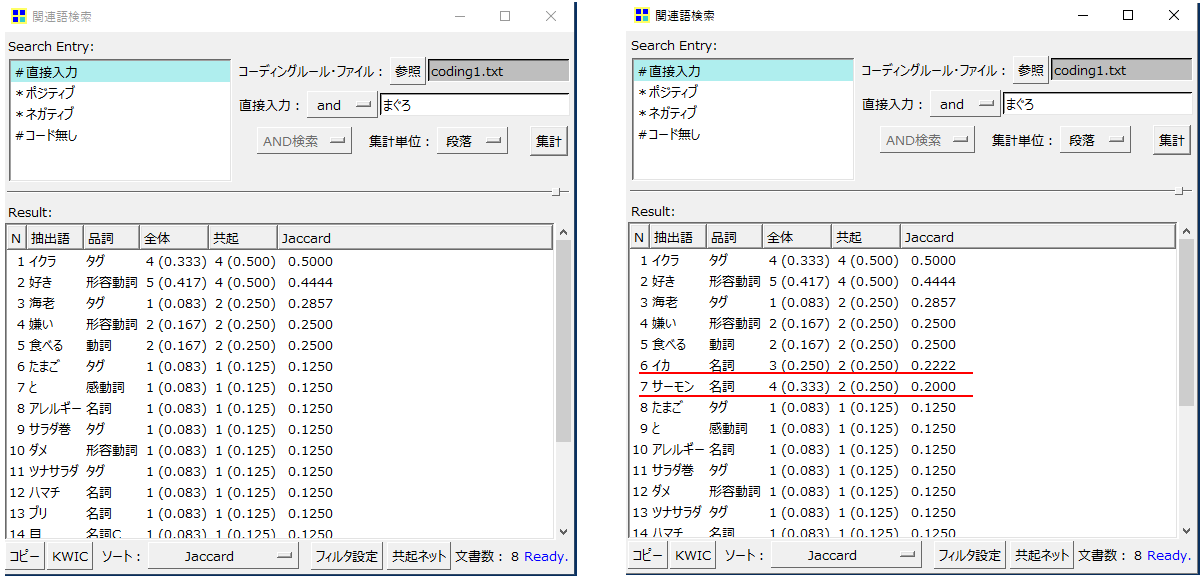
・左側がデフォルトの状態
・右側が「条件付き確率が低下する語も表示」した状態です。

　これまではなかった「イカ」「サーモン」が出現していることがわかります。
　基本的には条件付き確率が低下する語も表示した方がよいと思います。なぜデフォルトで除外されるのか？

　結果はデフォルトでJaccard係数降順で表示されます。
　想像ですが、このJaccard係数の算出式に母集団の概念がないからだろうと思います。Jaccard係数は「条件付き確率」とあわせて後述します。

各種係数

「まぐろ」と「好き」の関係

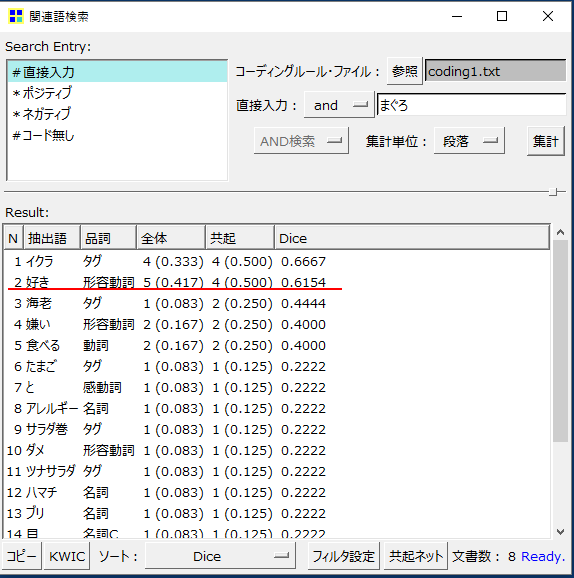
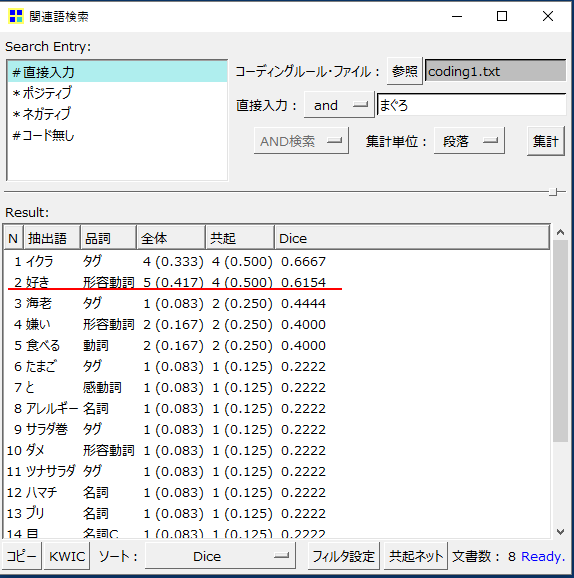
画像の内容を読んでみます。

・全体列の数値
　「好き」という「語」が出現する段数です。５「段」あります。

・全体列カッコ内の数値
　0.417＝５「段」(語が出現する段数) ÷１２「段」(分析対象テキスト」全体の「段」数)です。
　「好き」を含む「段」の出現確率といってよいと思います。

　

　「段」数＝回答者数になっているので、全回答者のうち約４０％が「好き」という「語」を使用した、といえます。

　「段」で集計するメリットは「段」数＝回答者数になっていることです。サッと全回答者のうち、何パーセントという数字を導き出すことができます。

共起

テキスト	「まぐろ」と共起
イクラ、サーモン、まぐろが好き。	している
好きなのはイクラとまぐろ。サバが嫌い。	している
鯛とまぐろが好き。エビはアレルギーがあるからダメ。	している
まぐろ、サラダ巻とかも好きです。イカは固いので食べない。	している
イカとかエビのようなあっさりしたネタが好き。サバが苦手。	していない

　「共起」が「まぐろ」との関連を示します。

　現在の集計単位は「段」です。
　「共起」というのは、同一の「段」のなかで「まぐろ」と「好き」の両方が出現していること、このように定義できます。
　「段」ということは、例えば「まぐろは嫌い。サーモンが好き。」このような場合でも「共起」しています。

・表の１段目から４段目までは「共起」している
・５段目は「まぐろ」が出現しないので「共起」していない
　従って「共起」の「段」数は４になります。

　カッコ内の0.500は、４段（共起している段数）÷８（「まぐろ」が出現する段数）で計算できます。ここでも「段」数＝回答者数ですから、「まぐろ」という「語」を使用した８人のうち５０％が「好き」という「語」を使用したといえます。

　ただし「まぐろ」が「好き」と答えた回答者が４人いる、このような断定はできません。
　というのは「好きではない」とか「まぐろは嫌い。サーモンが好き。」の回答が含まれる可能性があるからです。ここのところがテキストマイニングの難しいところです。

Jaccard

N	抽出語	品詞	全体	共起	Jaccard
12	好き	形容動詞	5 (0.417)	4 (0.500)	0.4444

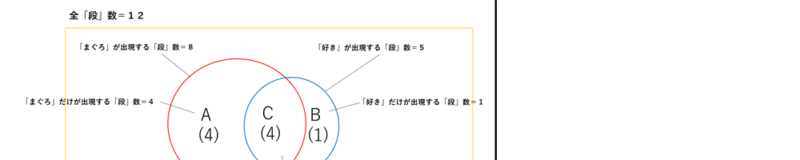
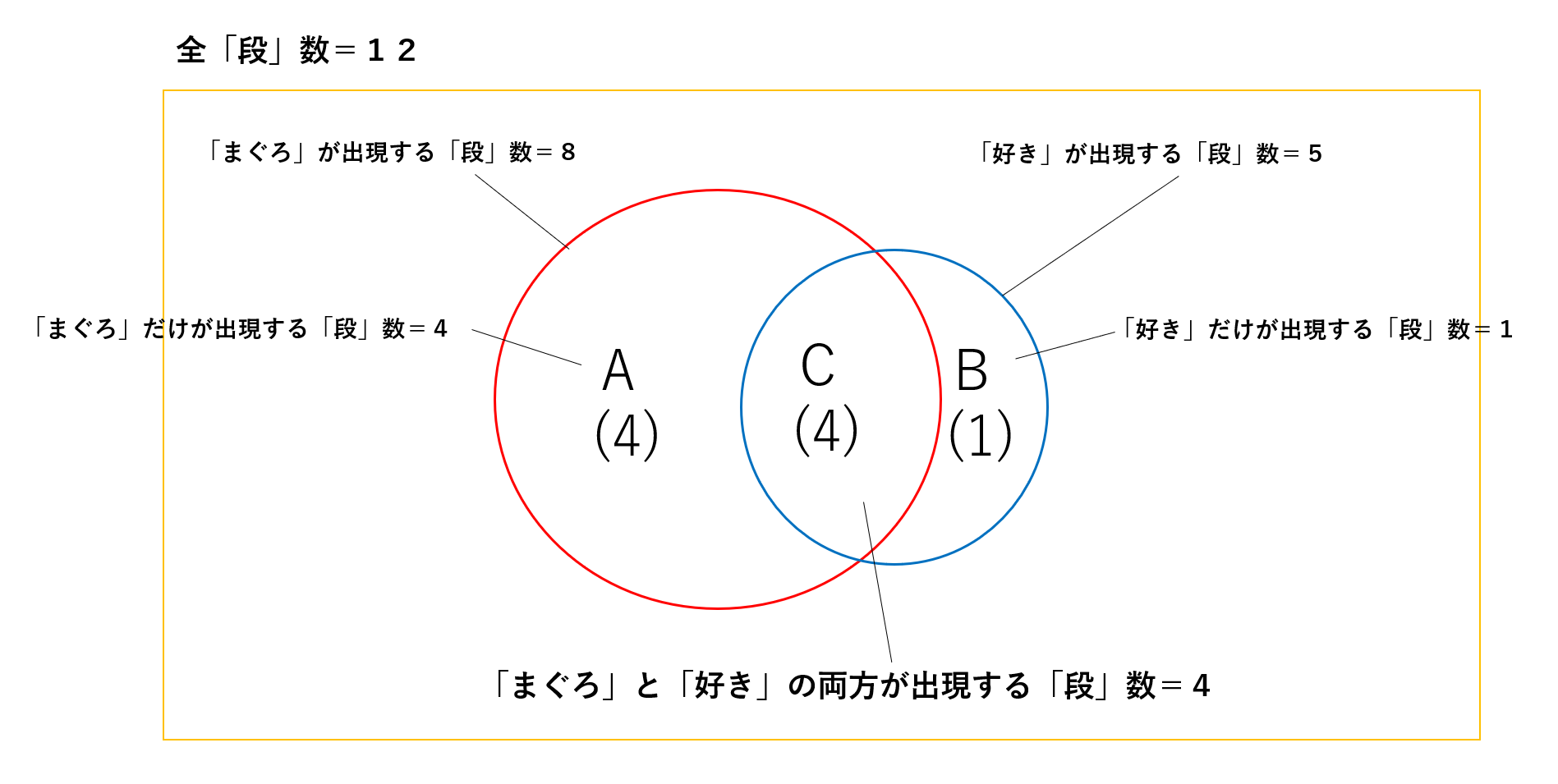
＜計算式＞
・「まぐろ」が出現する段「数」＝８（赤い円の集合）
・「好き」が出現している「段」数＝５（青い円の集合）
・「まぐろ」と「好き」が共起している「段」数＝４（図のＣの部分）

・図のＡの部分は４（８－４）
・図のＢの部分は１（５－４）
・図のⅭの部分は４
・母集合数は９（Ａ＋Ｂ＋Ｃ）

・分母＝９（Ａ＋Ｂ＋Ｃ）
・分子＝４（Ｃ：共起している「段」数）
・Jaccard＝４÷９＝0.4444

　Jaccard係数はＡとＢの段数に依存します。
　Ｃの部分（共起の回数）が大きくても、よりＡとＢの部分（分母に含まれる部分）がより大きければJaccard係数は低下します。

　つまり、ＡとＢの部分が大きいということは頻出語（出現回数が非常に多い語）だといえます。
　Ｃの部分が大きい（共起回数が多い）にもかかわらずJaccard係数を降順にならべると順位が低いという現象が起こります。

　Jaccard係数はあくまでも係数（分母に依存する）です。共起の回数とJaccard係数が常に正比例するとは限りません。
　このあたりに感覚的な矛盾を感じることがあります。そのため「条件付き確率が低下する語も表示」を登場させた意味があるように思います。

　Jaccard係数は母集団数（分析対象テキストの全「段」数合計、今回は１２「段」）に依存しません。

　従って、母集合数（回答者数）が1,000であっても「まぐろ」と「イクラ」のJaccard係数は0.4444のままです。やはりここでも「条件付き確率が低下する語も表示」の意味があるように思います。

確率差（条件付き確率）

　「確率差」とは共起率と出現率の差です。
　「条件付き確率が低下する語も表示」でフィルターされている状態では確率差が０以下マイナスの「語」が表示から除外されます。

　そういう理由で「まぐろ」で検索したとき、「イカ」「サーモン」が表示されませんでした。

　想像ですが、デフォルトで「条件付き確率が低下する語も表示」しないことで、Jaccard係数に含まれない母集団数の概念を取り入れたのだろう思います。

　共起率が低くなる要因は、分母の「まぐろ」が出現する「段」数Ａの部分が大きいときです。
　共起している相手の「語」の出現率が高くなる要因はＢの部分が大きいときです。

・Ａの部分が大きすぎる
・Ｂの部分が大きすぎる

　そうなると、Jaccard係数が大きく低下することがあります。そこで、確率差を利用して目隠しをしているようです。

　この確率差ゼロ以下が「条件付き確率」の条件の部分に該当します。

　ところが、共起している相手の「語」の出現率が高くなる要因には母集団数が小さいときがあります。

　現在の母集団数は１２ですが、仮に母集団数が１０の場合、「好き」の出現率は0.500になり、Jaccard係数0.4444を超えるのでデフォルトでは結果から除外されます。

　従って、基本的には「条件付き確率が低下する語も表示」するほうがよいのだろうと思います。

その他の係数

＜確率比＞
　共起率÷出現率

＜Dice＞
　「まぐろ」が出現する段「数」＝８（赤い円の集合）
　「好き」が出現している「段」数＝５（青い円の集合）
　「まぐろ」と「好き」が共起している「段」数＝４（Ｃの部分）
　分母＝１３（８＋５）
　分子＝８（４×２）
　Dice＝８÷１３＝0.6154

　分母が２集合（Jaccardとくらべると共起部分のＣをマイナスしない）の合計、分子を共起している部分の２倍にするから、共起している「語」の平均と考えてよさそうです。

　Jaccard係数と比較してＡの部分、Ｂの部分の依存度が低下します。結果的には各「語」のDice係数間の差異がJaccard係数よりも小さくなり、わかりにくくなりような弱点を感じます。

＜Ochiai＞
　「まぐろ」が出現する段「数」＝８
　「好き」が出現している「段」数＝５
　「まぐろ」と「好き」が共起している「段」数＝４
　√（４÷８）×√（４÷５）＝0.6325
　エクセル計算式は sqrt(4/8)*sqrt(4/5)
　平方根と平方根の積、ここまでくるとどのように理解すればよいのか・・・

＜Log Likelihood＞
　対数尤度比というものらしく、説明は不可能です。

＞KHcoder 13.　関連語検索(第2回)