Coding(KHcoder) 6 カイ2乗値
カイ2乗値とは何か?解るようで解りにくいような解説と、カイ2乗値の計算ロジックについて
カイ2乗値
カイ2乗検定
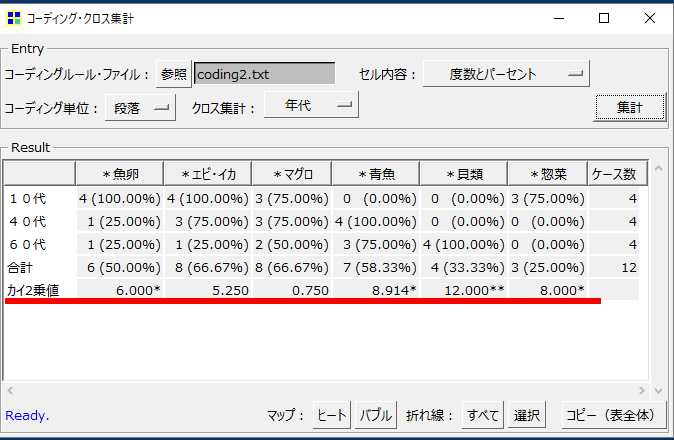
コーディング・クロス集計表の最下段に算出される「カイ2乗値」とは?
カイ2乗検定という独立性検定のことです。
・好きなすしネタデータのコード「魚卵」は合計6回出現しています。
もしもコード「魚卵」の出現が年代から独立しているという仮説が成立するなら、
・出現回数6回÷年代3階級=2
確率的に「コード」魚卵は各年代3階級(10代・40代・60代)に各2回ずつ出現するはずです。
ところが実際には10代に偏って出現しています。
このように、どこかの年代に偏って出現しているということを独立ではないといいます。
つまりコード「魚卵」と、それが出現する年代とのあいだには、何かの関係があるのだろうということです。
各コードと各年代との関係が独立なのか、そうではないのかを検定することがカイ2乗検定です。検定にはカイ2乗値から算出するp値を使用します。
カイ2乗検定
| さいころの目 | 実際の出現回数 | 期待度 |
| 1 | 0 | 100 |
| 2 | 120 | 100 |
| 3 | 120 | 100 |
| 4 | 120 | 100 |
| 5 | 120 | 100 |
| 6 | 120 | 100 |
1個のサイコロを合計600回ふります。
1つの目がでる確率は6分の1ですから合計600回ふれば目は各100回になるのだろうと思います。これが「期待度」です。
ところが、上表のように1の目が全く出現しなかったらどうでしょうか。
上表をカイ2乗検定すると「出目が独立ではありません」ということをp値が教えてくれるわけです。
① サイコロが正六面体ではない。
② サイコロの転がる面が水平ではない。
③ 思いのままに目を出すことができるサイコロ名人がふっている。
このように、サイコロの場合は独立ではない理由をいくつか考えることができます。
テキストマイニングでは、アンケート自体の問題で回答者の声を反映していないとか、マグロ祭りの真っ最中にアンケートを実施したなど、独立ではない理由を考えることができます。
しかし、コンピューターはアンケートがどのような状況で行われたのかなどを計算には全く考慮しません。
ただ「コード」と「外部変数」のと関係を粛々と計算するだけです。
独立ではない理由が「コード」と「外部変数」のと関係にあるのか、もしかするとアンケート自体の問題なのか?結果をみながら考えてみることをオススメします。
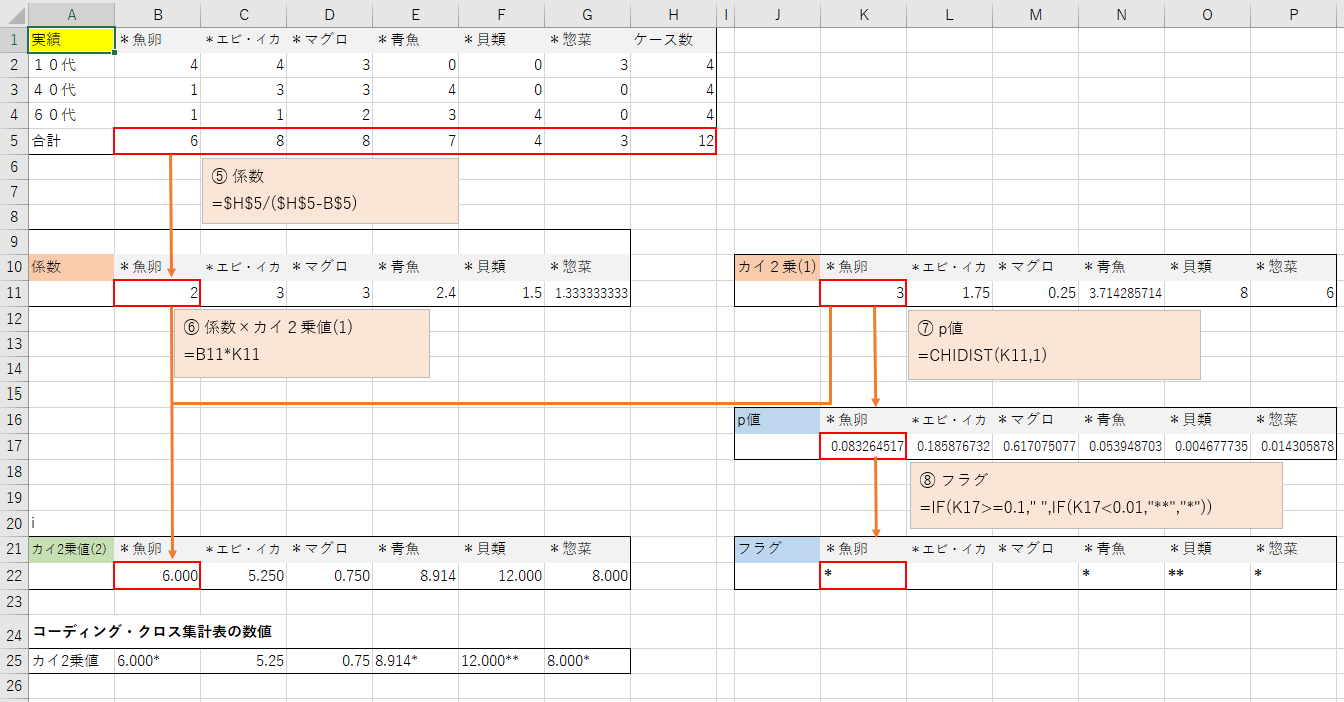
カイ2乗値計算ロジック
方程式:カイ2乗値=(実績値-期待度)^2÷期待度
方程式に従い計算をします。
① 各セルへ平均値を入れます。各セルの数値を縦合計値で割ります。この平均値が期待度です。
② 実績値と期待度との差分を計算します。
③ 実績値と期待度との差分を2乗します。
④ 実績値と期待度との差分の2乗を期待度で割ります。縦合計を算出します。
計算結果がコーディング・クロス集計表の値と一致しません。更に計算をすすめます。
⑤ ケース数合計をケース数合計と縦合計との差分で割ります。
⑥ ④で算出したカイ2乗(1)と⑤係数をかけ合わせます。この数値がコーディング・クロス集計に記載されているカイ2乗値です。
ここからp値の計算
⑦ ④で算出したカイ2乗(1)からp値を算出します。
⑧ p値にたいして「*」を付与します。
・p値>=0.1のとき「*」はなし。0.01<=p値<0.1のとき「*」
・p値<0.01のとき「**」です。
・「*」の数が多いほど独立ではないことを示します。
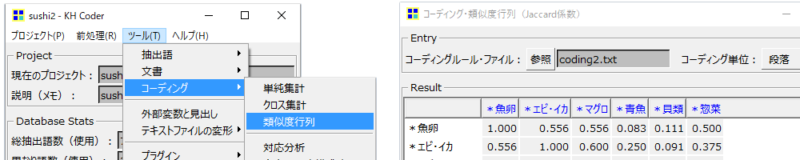
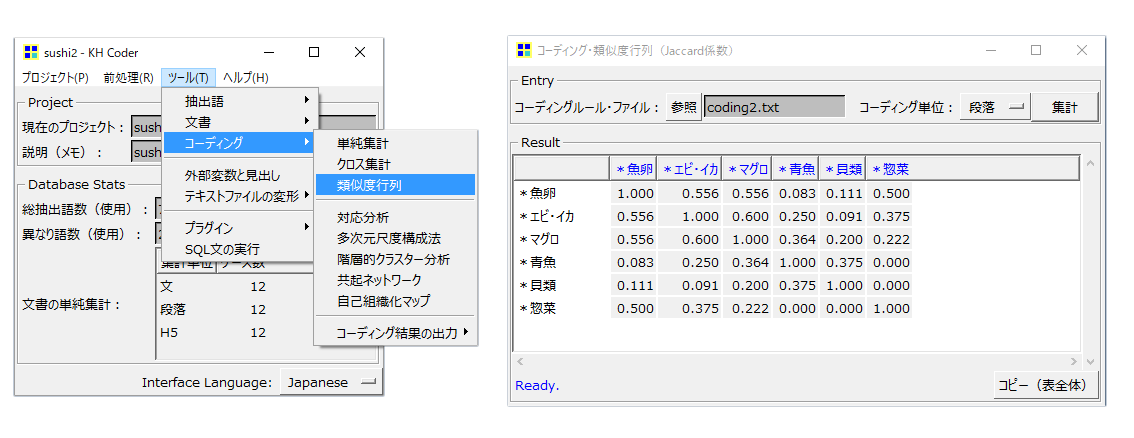
類似度行列
手順
・「ツール」→「コーディング」→「類似度行列」の順にクリックして
・「集計」ボタンを押します。
「コード」×「コード」のマトリクスが表示されます。これは対応分析やクラスター分析につかう「コード」と「コード」の距離を示すものだろうとピンときます。
method_dist <- "binary" method_clst <- "ward" library(amap) dj <- Dist(d,method=method_dist)
| *魚卵 | *エビ・イカ | *マグロ | *青魚 | *貝類 | |
| *エビ・イカ | 0.4444444 | ||||
| *マグロ | 0.4444444 | 0.4 | |||
| *青魚 | 0.9166667 | 0.75 | 0.6363636 | ||
| *貝類 | 0.8888889 | 0.9090909 | 0.8 | 0.625 | |
| *惣菜 | 0.5 | 0.625 | 0.7777778 | 1 | 1 |
Rから出力される距離計算の結果はこのようになります。
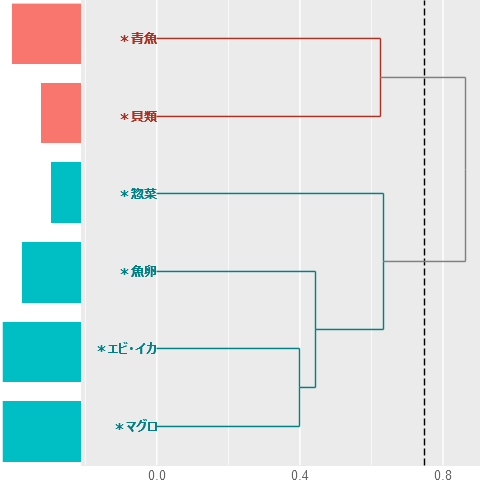
クラスターは「コード」とコード」の距離が短い順にしたがいつくられていきます。
「エビ・イカ」と「マグロ」がまっ先に群をつくり「魚卵」が次にくっつきます。計算結果の通りです。
数値の違い
| *魚卵 | *エビ・イカ | *マグロ | *青魚 | *貝類 | |
| *エビ・イカ | 0.556 | ||||
| *マグロ | 0.556 | 0.6 | |||
| *青魚 | 0.083 | 0.25 | 0.364 | ||
| *貝類 | 0.111 | 0.091 | 0.2 | 0.375 | |
| *惣菜 | 0.5 | 0.375 | 0.222 | 0 | 0 |
類似度行列結果が「コード」と「コード」の距離計算結果と違います。
表をよーく見ていると違いに気付きました。
・類似度行列=1-距離
つまり距離が近いほど類似度行列数値は大きくなる仕組みです。具体的な使用方法は不明です。